Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong góc AOC vẽ tia Ot sao cho O t / / A B .
Khi đó A ^ + A O t ^ = 180 ° (cặp góc trong cùng phía).
Suy ra A O t ^ = 180 ° − m ° .
Do đó C O t ^ = A O C ^ − A O t ^ = 360 ° − m ° + n ° − 180 ° − m ° = 180 ° − n °
Vậy C ^ + C O t ^ = n ° + 180 ° − n ° = 180 ° .
Suy ra CD // Ot (vì có cặp góc trong cùng phía bù nhau).
Do đó AB // CD(vì cùng song song với Ot).

theo giả thiết
\(\angle\left(A1\right)-2\angle\left(A2\right)=\angle\left(B1\right)-2\angle\left(B2\right)\)
\(< =>180-3\angle\left(A2\right)=180-3\angle\left(B2\right)\)
\(< =>-3\angle\left(A2\right)+3\angle\left(B2\right)=0\)
\(< =>-3\left[\angle\left(A2\right)-\angle\left(B2\right)\right]=0\)
điều này xảy ra\(< =>\angle\left(A2\right)=\angle\left(B2\right)\)
2 góc ở vt so le trong \(=>dpcm\)

dễ thôi, a // b . Vì:
A1 + B2 = 180 độ (2 góc trong cùng phía bù nhau)
1 dữ kiện thôi cũng đủ rùi

Ta có: \(\frac{a+1}{b+1}-\frac{a}{b}=\frac{b\left(a+1\right)}{b\left(b+1\right)}-\frac{a\left(b+1\right)}{b\left(b+1\right)}=\frac{ab+b-ab-a}{b\left(b+1\right)}=\frac{b-a}{b\left(b+1\right)}=\frac{1}{b\left(b+1\right)}\left(b-a\right)\)
Vì a < b => (b - a) > 0
\(\Rightarrow\frac{1}{b\left(b+1\right)}\left(b-a\right)>0\)\(\Rightarrow\frac{a+1}{b+1}-\frac{a}{b}>0\)\(\Rightarrow\frac{a+1}{b+1}>\frac{a}{b}\)
b) Cho f(x)=ax3+bx2+cx+d , trong đó a,b,c,d là hằng số và thoả mãn: b=3a+c, Chứng tỏ rằng: f(1)=f(2)

Thay b = 3a + c vào f(x) ta được:
f(x) = ax3 + (3a+c)x2 + cx + d
⇒ f(1) = a.13 + 3a + c.12+ c.1 + d
= a + 3a + c + c + d
= 4a + 2c + d
= 4a + 2c + d (1)
f(2) = a.23 + 3a + c.22 - c.2 + d
= 8a + 3a + 4c - 2c + d
= 4a + 2c + d (2)
Từ (1) và (2) ➩ f(1) = f(2) [= 4a + 2 + d]
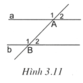


Ta có A 1 ^ + A 2 ^ + B 2 ^ = a ° ⇒ B 2 ^ = a ° − 180 ° (1)
B 1 ^ + B 2 ^ + A 1 ^ = b ° ⇒ A 1 ^ = b ° − 180 ° (2)
Từ (1) và (2), suy ra: B 2 ^ + A 1 ^ = a ° + b ° − 360 ° = 540 ° − 360 ° = 180 ° .
Mặt khác A 2 ^ + A 1 ^ = 180 ° (kề bù) nên B 2 ^ + A 1 ^ = A 2 ^ + A 1 ^ = 180 ° .
Suy ra B 2 ^ = A 2 ^ . Do đó a // b vì có cặp góc đồng vị bằng nhau