Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha mình biếng á chứ khog có j đou=)
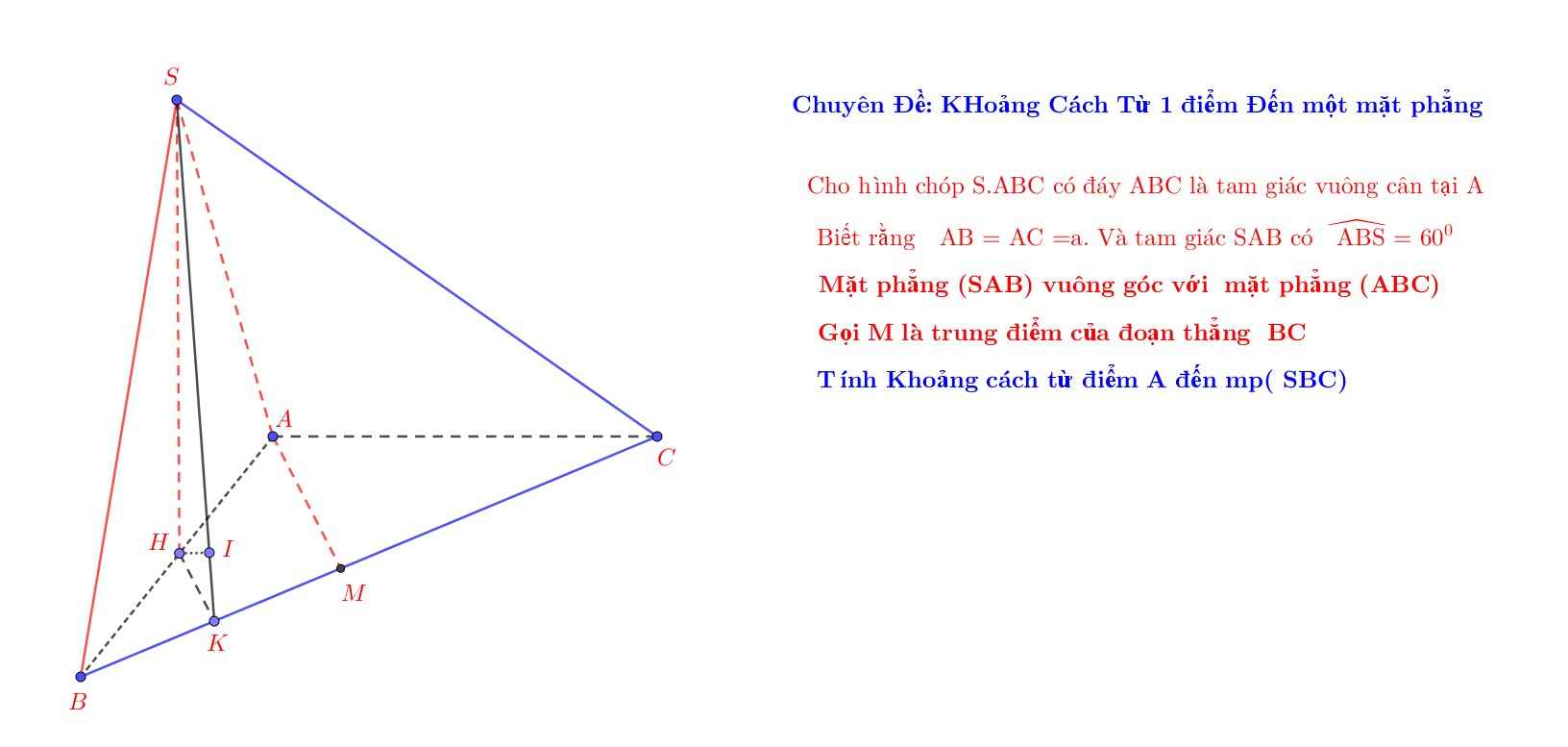
Ta có : \(\left\{{}\begin{matrix}CA\perp AB\\\left(ABC\right)\perp\left(SAB\right)\\\left(ABC\right)\cap\left(SAB\right)=AB\end{matrix}\right.\) \(\Rightarrow CA\perp\left(SAB\right)\)
Kẻ \(AK\perp SB\) và \(AH\perp CK\) tại H.
Ta có : \(\left\{{}\begin{matrix}SB\perp AK\\SB\perp CA\end{matrix}\right.\) \(\Rightarrow SB\perp\left(ACK\right)\Rightarrow SB\perp AH\)
Do : \(\left\{{}\begin{matrix}AH\perp CK\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=AH\)
Xét t/g ABK , ta có : AK = AB
=> \(sin\widehat{ABK}=\alpha sin60^o=\dfrac{a\sqrt{3}}{2}\)
Xét t/g ACK , ta có : \(\dfrac{1}{AH^2}=\dfrac{1}{AK^2}+\dfrac{1}{AC^2}=\dfrac{7}{3a^2}\Rightarrow AH=\dfrac{a\sqrt{21}}{7}\)

Bạn ơi, bạn kiểm tra lại đề giúp mình nha, đoạn "...thỏa mãn AC=34H"


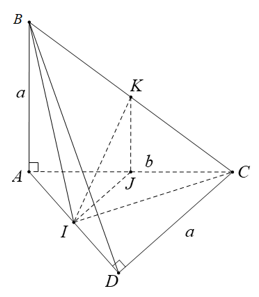
Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)
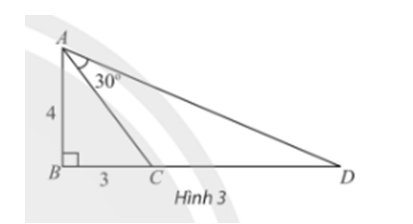







Xét tam giác ABC vuông tại B có:
\(\tan \widehat {BAC} = \frac{3}{4}\)
Suy ra, \(\tan \widehat {BAD} = \tan \left( {\widehat {BAC} + \widehat {CAD}} \right) = \tan \left( {\widehat {BAC} + {{30}^0}} \right)\)
\( = \frac{{\tan \widehat {BAC} + \tan {{30}^0}}}{{1 - \tan \widehat {BAC}.\tan {{30}^0}}} = \frac{{\frac{3}{4} + \frac{{\sqrt 3 }}{3}}}{{1 - \frac{3}{4}.\frac{{\sqrt 3 }}{3}}} \approx 2,34\)
Xét tam giác vuông ABD vuông tại B có:
\(\begin{array}{l}BD = AB.\tan \widehat {BAD} = 4.2,34 \approx 9,36\\ \Rightarrow CD = BD - BC \approx 9,36 - 3 \approx 6,36\end{array}\)