Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có: \(\overrightarrow{AC}=(x_C-2,y_C-6)\) ;\(\overrightarrow{AQ}=(-1,-6)\)
Vì $A,C,Q$ thẳng hàng nên tồn tại $k$ sao cho:
\(\overrightarrow{AC}=k\overrightarrow{AQ}\Leftrightarrow (x_C-2,y_C-6)=k(-1,-6)\)
\(\Rightarrow \frac{x_C-2}{-1}=\frac{y_C-6}{-6}\Rightarrow y_C=6x_C-6\).
Tọa độ \(C(c,6c-6)\)
$M$ là trung điểm $BC$ nên: \(\left\{\begin{matrix} \frac{x_B+c}{2}=1\\ \frac{y_B+6c-6}{2}=5\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} x_B=2-c\\ y_B=16-6c\end{matrix}\right.\). Tọa độ \(B(2-c,16-6c)\)
---------------------
Mặt khác. Gọi tọa độ $P$ là \((a,\frac{1-a}{2})\)
$H$ là trung điểm $PQ$ nên:
\(\left\{\begin{matrix} x_H=\frac{x_P+x_Q}{2}=\frac{a+1}{2}\\ y_H=\frac{y_P+y_Q}{2}=\frac{1-a}{4}\end{matrix}\right.\). Tọa độ \(H(\frac{a+1}{2}; \frac{1-a}{4})\)
Ta có:
\(BH\perp AQ\Rightarrow \overrightarrow{BH}.\overrightarrow{QA}=0\)
\(\Leftrightarrow (\frac{a+1}{2}-2+c, \frac{1-a}{4}-16+6c).(1,6)=0\)
\(\Leftrightarrow \frac{a+1}{2}-2+c+6(\frac{1-a}{4}-16+6c)=0\)
\(\Leftrightarrow 37c-a-96=0(1)\)
\(AH\perp MC\) \(\Rightarrow \overrightarrow{AH}.\overrightarrow{MC}=0\)
\(\Leftrightarrow (\frac{a-3}{2}, \frac{-a-23}{4})(c-1, 6c-11)=0\)
\(\Leftrightarrow \frac{(a-3)(c-1)}{2}-\frac{(a+23)(6c-11)}{4}=0\)
\(\Leftrightarrow 9a-4ac-144c+259=0(2)\)
Giải hệ (1)(2) ta có pt vô nghiệm nên không tồn tại tọa độ B,C
Bạn check lại đề nhé, số quá xấu :)

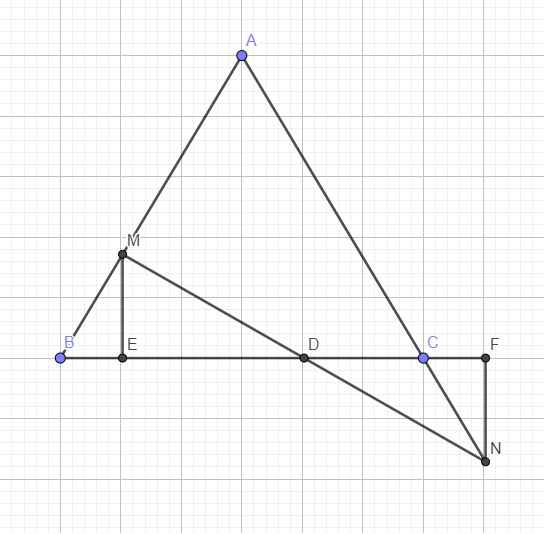
Gọi D là giao điểm MN và BC
Từ M kẻ ME vuông góc BC, từ N kẻ NF vuông góc BC
\(\widehat{B}=\widehat{C}=\widehat{NCF}\Rightarrow\Delta MBE=\Delta NCF\left(ch-gn\right)\)
\(\Rightarrow ME=NF\)
\(\Rightarrow\Delta MED=\Delta NFD\)
\(\Rightarrow MD=ND\) hay D là trung điểm MN
\(\Rightarrow D\left(-1;3\right)\Rightarrow\overrightarrow{ED}=\left(2;4\right)=2\left(1;2\right)\)
Phương trình BC (hay ED) có dạng:
\(2\left(x+3\right)-1\left(y+1\right)=0\Leftrightarrow2x-y+5=0\)
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+4=0\\2x-y+5=0\end{matrix}\right.\) \(\Rightarrow B\left(-4;-3\right)\)
\(\Rightarrow\overrightarrow{BM}=\left(3;4\right)\) \(\Rightarrow cosB=\dfrac{\left|3.1+4.2\right|}{\sqrt{3^2+4^2}.\sqrt{1^2+2^2}}=\dfrac{11\sqrt[]{5}}{25}\)
Do C thuộc BC nên tọa độ dạng: \(C\left(c;2c+5\right)\Rightarrow\overrightarrow{NC}=\left(c+1;2c+12\right)\)
\(cosC=cosB=\dfrac{11\sqrt{5}}{25}=\dfrac{\left|1.\left(c+1\right)+2\left(2c+12\right)\right|}{\sqrt{1^2+2^2}.\sqrt{\left(c+1\right)^2+\left(2c+12\right)^2}}\)
\(\Leftrightarrow c^2+10c-96=0\Rightarrow\left[{}\begin{matrix}c=6\Rightarrow C\left(6;17\right)\\c=-16\Rightarrow C\left(-16;-27\right)\end{matrix}\right.\)
(Loại \(C\left(-16;-27\right)\) do D nằm giữa B và C)
Viết phương trình AB (qua M và B), viết phương trình AC (qua N và C). Tọa độ A là giao AB và AC