Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo không phụ thuộc vào khối lượng của lò xo.

Chọn C.
Khi nén lực 10 N
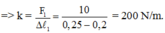
Khi lực đàn hồi là F2 = 8 N thì độ biến dạng của lò xo:
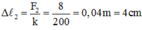
Suy ra chiều dài lò xo khi đó là:
ℓ2 = ℓ0 ± ∆ℓ2 = 21 cm hoặc 29 cm.

Ta có: l 0 = 20 c m
+ Khi l = l 1 = 24 c m thì độ dãn của lò xo Δ l 1 = l 1 − l 0 = 24 − 20 = 4 c m = 0 , 04 m
=> Độ lớn của lực đàn hồi
F d h 1 = 5 N = k . Δ l 1 ↔ 5 = k .0 , 04 → k = 125 N / m
+ Gọi l 2 , Δ l 2 là chiều dài của lò xo và độ dãn của lò xo khi lực đàn hồi của lò xo là: F d h 2 = 10 N
Ta có:
F d h 2 = k Δ l 2 ↔ 10 = 125. Δ l 2 → Δ l 2 = 0 , 08 m = 8 c m
=> Chiều dài của lò xo:
l 2 = l 0 + Δ l 2 = 20 + 8 = 28 c m
Đáp án: B

a) Vị trí lực đàn hồi cân bằng với trọng lực:
kx0 = mg => x0 = 0,02 m = 2 cm.
b) Vận tốc của vật tại vị trí lực đàn hồi cân bằng với trọng lực:
1/2 . k(xo)2 = ½k(vcb)2 => |vcb| = 0,2√5 m/s = 20√5 (cm/s).
a. Ở vị trí cân bằng thì lực đàn hồi cân bằng với trọng lượng
\(\Rightarrow F_{đh}=P\Rightarrow k.\Delta l_0=mg\)
\(\Rightarrow \Delta l_0=\dfrac{mg}{k}=\dfrac{0,4.10}{200}=0,02m=2cm\)
b. Vị trí đó chính là vị trí cân bằng.
Chọn gốc thế năng ở vị trí cân bằng.
Thả vật ở vị trí lò xo không giãn \(\Rightarrow x_1=2cm\)
Áp dụng định luật bảo toàn cơ năng ta có:
\(\dfrac{1}{2}.k.x_1^2=\dfrac{1}{2}.m.v^2\)
\(\Rightarrow v = x_1.\sqrt{\dfrac{k}{m}}=2.\sqrt{\dfrac{200}{0,4}}==20\sqrt 5 (cm/s)\)

Đáp án D.
Ta có: Wt = ½ k(∆ℓ)2 = ½ .100.(0,05)2 = 0,125 J.


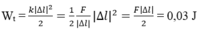
Chọn D.
Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo không phụ thuộc vào khối lượng của lò xo.