

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tham Khảo:
a) u2 = u1 + 500 = 8000 + 500 = 8500
u3 = u2 + 500 = 8500 + 500 = 9000
v2 = v1 + v1. 0,07 – v1 (1 + 0,07) = v1.1,07 = 6000.1,07 = 6420
v3 = v2 + v2.0,07 = v2(1 + 0,07) = v2.1,07 = 6420.1,07 = 6869,4
b) Theo giả thiết của bài toán , ta có:
u1 = 8000 và un + 1 = un + 500 với mọi n ≥ 1 (1)
v1 = 6000 và vn + 1 = vn + vn.0,07 = vn(1 + 0,07) = vn.1,07 với mọi n ≥ 1 (2)
Từ (1) suy ra (un)là một cấp số cộng với công sai d=500 và số hạng đầu u1 = 8000
Số hạng tổng quát: un = 8000 + (n – 1).500 = 7500 + 500nTừ (2) suy ra (vn) là một cấp số nhân với công bội q=1,07 và số hạng đầu v1 = 6000
Số hạng tổng quát: vn = 6000.(1,07)n - 1
c) Kí hiệu A20 và B20 tương ứng là số tiền công( tính theo đơn vị đồng) cần trả theo cách tính giá của cơ sở B. Từ kết quả phần b) ta có:
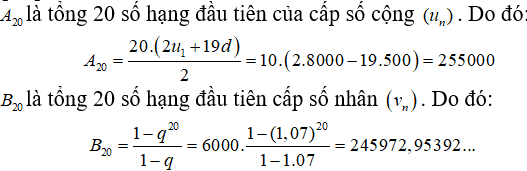
Từ đó, nếu cần khoan giếng sâu 20m thì nên thue cơ sở B.
d) Kí hiệu A25 và B25 tương ứng là số tiền công ( tính theo đơn vị đồng) cần trả theo cách tính giá của cơ sở A và theo cách tính giá của cơ sở B.
Bằng cách tương tự như ở phần c) ta tình được A25 = 350000 và B25 = 37494,22629...
Do đó, nếu cần khoan giếng sâu 25m thì nên thuê cơ sở A.

Hàm số \(T\left( x \right)\) xác định trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số \(T\left( x \right)\) xác định trên từng khoảng \(\left( {0;0,7} \right),\left( {0,7;20} \right)\) và \(\left( {20; + \infty } \right)\) nên hàm số liên tục trên các khoảng đó.
Ta có: \(T\left( {0,7} \right) = 10000\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0,{7^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to 0,{7^ + }} \left( {10000 + \left( {x - 0,7} \right).14000} \right) = 10000 + \left( {0,7 - 0,7} \right).14000 = 10000\\\mathop {\lim }\limits_{x \to 0,{7^ - }} T\left( x \right) = \mathop {\lim }\limits_{x \to 0,{7^ - }} 10000 = 10000\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to 0,{7^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to 0,{7^ - }} T\left( x \right) = 10000\) nên \(\mathop {\lim }\limits_{x \to 0,7} T\left( x \right) = 10000 = T\left( {0,7} \right)\).
Vậy hàm số \(T\left( x \right)\) liên tục tại điểm \({x_0} = 0,7\).
Ta có: \(T\left( {20} \right) = 10000 + \left( {20 - 0,7} \right).14000 = 280200\)
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {{20}^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to {{20}^ + }} \left( {280200 + \left( {x - 20} \right).12000} \right) = 280200 + \left( {20 - 20} \right).12000 = 280200\\\mathop {\lim }\limits_{x \to {{20}^ - }} T\left( x \right) = \mathop {\lim }\limits_{x \to {{20}^ - }} \left( {10000 + \left( {x - 0,7} \right).14000} \right) = 10000 + \left( {20 - 0,7} \right).14000 = 280200\end{array}\)
Vì \(\mathop {\lim }\limits_{x \to {{20}^ + }} T\left( x \right) = \mathop {\lim }\limits_{x \to {{20}^ - }} T\left( x \right) = 280200\) nên \(\mathop {\lim }\limits_{x \to 20} T\left( x \right) = 280200 = T\left( {20} \right)\).
Vậy hàm số \(T\left( x \right)\) liên tục tại điểm \({x_0} = 20\).
Vậy hàm số \(T\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\).

Tham khảo:
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 6 + 7.5 \times 10 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.5\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chưa mốt là \(\left[ {10;15} \right)\).

Gọi số ngày anh Hải cần phải tiết kiệm là x
Ngày 1 anh hải tiết kiệm được 5000(đồng)
Ngày 2 anh Hải tiết kiệm được 5000+2000(đồng)
Ngày 3 anh Hải tiết kiệm được 5000+2*2000(đồng)
...
Ngày x anh Hải tiết kiệm được 5000+(x-1)*2000(đồng)
Theo đề, ta có:
\(5000+5000+2000+5000+2\cdot2000+...+5000+\left(x-1\right)\cdot2000>=3840000\)
=>\(x\cdot5000+2000\left(1+2+...+x-1\right)>=3840000\)
=>\(5000x+2000\cdot\dfrac{x\left(x-1\right)}{2}>=3840000\)
=>\(5x+\dfrac{2x\left(x-1\right)}{2}>=3840\)
=>\(5x+x^2-x>=3840\)
=>\(x^2+4x-3840>=0\)
=>(x-60)(x+64)>=0
=>\(\left[{}\begin{matrix}x>=60\\x< =-64\left(loại\right)\end{matrix}\right.\)
Vậy; anh hải cần để dành 60 ngày để đủ số tiền mua đôi giày

Có \(7! = 5040\) cách sắp xếp 7 bạn ngồi vào 7 chiếc ghế \( \Rightarrow n\left( \Omega \right) = 5040\)
Gọi \(A\) là biến cố: “Bình vẫn ngồi đúng ghế cũ của mình”, \(B\) là biến cố “Minh vẫn ngồi đúng ghế cũ của mình”.
Vậy \(AB\) là biến cố “Cả Bình và Minh vẫn ngồi đúng ghế cũ của mình”, \(A \cup B\) là biến cố “Có ít nhất một trong hai bạn Bình và Minh vẫn ngồi đúng ghế cũ của mình”.
Xếp chỗ cho Bình ngồi đúng ghế cũ của mình có 1 cách.
Xếp chỗ cho 6 bạn còn lại có \(6! = 720\) cách.
\( \Rightarrow n\left( A \right) = 1.720 = 720 \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{720}}{{5040}} = \frac{1}{7}\)
Xếp chỗ cho Minh ngồi đúng ghế cũ của mình có 1 cách.
Xếp chỗ cho 6 bạn còn lại có \(6! = 720\) cách.
\( \Rightarrow n\left( B \right) = 1.720 = 720 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left(\Omega \right)}} = \frac{{720}}{{5040}} = \frac{1}{7}\)
Xếp chỗ cho cả Bình và Minh ngồi đúng ghế cũ của mình có 1 cách.
Xếp chỗ cho 5 bạn còn lại có \(5! = 120\) cách.
\( \Rightarrow n\left( {AB} \right) = 1.120 = 120 \Rightarrow P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}} = \frac{{120}}{{5040}} = \frac{1}{{42}}\)
\( \Rightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{1}{7} + \frac{1}{7} - \frac{1}{{42}} = \frac{{11}}{{42}}\)