Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
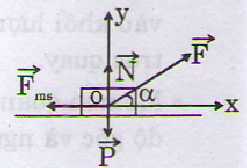
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


a) PT x1 có dạng tổng quát là: \(x=x_0+v_0t+\dfrac{1}{2}at^2\) nên chuyển động của vật 1 là chuyển động thẳng biến đổi đều.
Căn cứ theo phương trình ta có:
+ \(x_0=0\)
+ \(v_0=-8(m/s)\)
+ \(a=2(m/s^2)\)
Do \(v_0<0\) nên t = 0 thì vật chuyển động ngược chiều dương của trục toạ độ.
Do \(v_0\) ngược dấu với \(a\) nên chuyển động đang là chuyển động chậm dần đều.
PT x2 có dạng tổng quát: \(x=x_0+v.t\) nên chuyển động của vật 1 là chuyển động thẳng đều, căn cứ theo phương trình ta suy ra được:
+ \(x_{02}=12(m)\)
+ \(v_2=5(m/s)\)
Do \(v_2>0\) nên vật 2 đang chuyển động cùng chiều dương với trục toạ độ.
b) Khoảng cách 2 vật là:
\(\Delta x = |x_1-x_2|=|t_2-13t-12|\)
\(t=2(s)\) \(\Rightarrow \Delta x = |2-13.2-12|=36(m)\)
c) Pt vận tốc của vật 2 là:
\(v=v_0+a.t=-8+2.t\) (m/s)
Vật 2 đổi chiều chuyển động khi \(v=0\Rightarrow -8+2.t=0\Rightarrow t = 4(s)\)
Ban đầu, t= 0 thì vị trí vật 2 là: \(x_2=12+5.0=12(m)\)
Khi t = 4s thì vị trí vật 2 là: \(x_2'=12+5.4=32(m)\)
Quãng đường vật 2 đi được là: \(S_2=x_2'-x_2=43-12=20(m)\)
d) Lúc t = 3s, vận tốc vật 1 là: \(v_1=-8+2.3=-2(m/s)\)
Lúc này vật 1 có vận tốc là 2m/s và đang chuyển động chậm dần đều ngược chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
e) Lúc t = 6s, vận tốc vật 1 là: \(v_1=-8+2.6=4(m/s)\)
Lúc này vật 1 có vận tốc là 4m/s và đang chuyển động nhanh dần đều cùng chiều dương của trục toạ độ. Còn vật 2 vẫn đang chuyển động đều với vận tốc là 5m/s theo chiều dương trục toạ độ.
f) Quãng đường vật 1 đi được từ 2s đến 5s là:
\(|(5^2-8.5)-(2^2-8.2)|=3(m)\)

\(\overrightarrow{F_{ht}}=m.\overrightarrow{a_{ht}}\Rightarrow F_{ht}=m.a_{ht}\)
\(\overrightarrow{F_{msn}}=\mu.\overrightarrow{N}\Rightarrow F_{msn}=\mu mg\)
Có \(F_{ht}\le F_{msn}\Rightarrow m.a_{ht}\le\mu mg\)
\(\Leftrightarrow\omega^2.R\le\pi^2.\mu\)
\(\Leftrightarrow\pi^2.0,2\le\pi^2.\mu\Rightarrow\mu\ge0,2\)
Vậy để vât ko bị trượt thì \(\mu\ge0,2\)

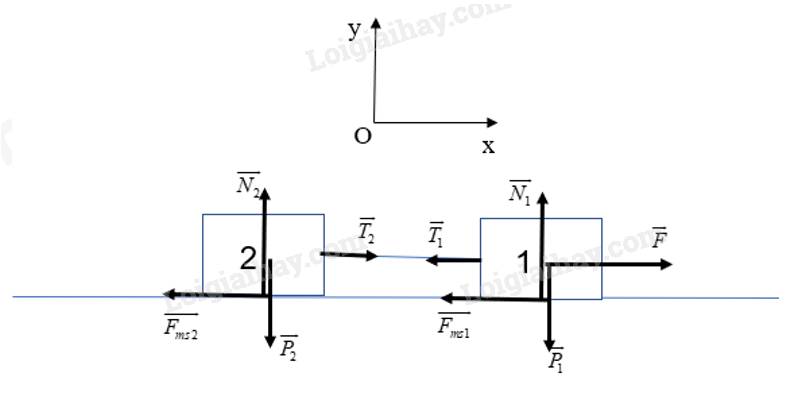
Chọn hệ quy chiếu như hình vẽ:
Theo định luật 2 Newton cho hệ vật, ta có:
\(\overrightarrow {{P_1}} + \overrightarrow {{P_2}} + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{F_{ms2}}} + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = ({m_1} + {m_2}).\overrightarrow a \) (1)
Chiếu (1) lên Ox, ta có
\(\begin{array}{l}F - {F_{ms1}} - {F_{ms2}} - {T_1} + {T_2} = ({m_1} + {m_2}).a\\ \Leftrightarrow F - \mu ({N_1} + {N_2}) = ({m_1} + {m_2}).a\end{array}\)
\( \Leftrightarrow a = \frac{{F - \mu ({N_1} + {N_2})}}{{{m_1} + {m_2}}}\) (2)
(do \({T_1} = {T_2}\))
Chiếu (1) lên Oy, ta có:
\(\begin{array}{l}{N_1} + {N_2} - {P_1} - {P_2} = 0\\ \Leftrightarrow {N_1} + {N_2} = {P_1} + {P_2}\\ \Leftrightarrow {N_1} + {N_2} = ({m_1} + {m_2}).g\end{array}\)
Thay \({N_1} + {N_2} = ({m_1} + {m_2}).g\) vào (2), ta có:
\(\begin{array}{l}a = \frac{{F - \mu .g({m_1} + {m_2})}}{{{m_1} + {m_2}}}\\ \Leftrightarrow a = \frac{{45 - 0,2.9,8.(5 + 10)}}{{5 + 10}}\\ \Leftrightarrow a = 1,04(m/{s^2})\end{array}\)
Xét vật 1
Theo định luật 2 Newton, ta có
\(\overrightarrow {{P_1}} + \overrightarrow {{N_1}} + \overrightarrow F + \overrightarrow {{F_{ms1}}} + \overrightarrow {{T_1}} = {m_1}.\overrightarrow a \) (3)
Chiếu (3) lên Ox, có
\(\begin{array}{l}F - {F_{ms1}} - {T_1} = {m_1}.a\\ \Leftrightarrow {T_1} = F - \mu {N_1} - {m_1}.a\end{array}\)
Chiếu (3) lên Oy, ta có \({N_1} = {P_1} = {m_1}.g\)
\(\begin{array}{l} \Rightarrow {T_1} = F - \mu {m_1}g - {m_1}.a\\ \Leftrightarrow {T_1} = 45 - 0,2.5.9,8 - 5.1,04\\ \Leftrightarrow {T_1} = 30(N)\end{array}\)
Vậy gia tốc của hai vật là 1,04 m/s2 và lực căng của dây nối là 30 N.

2)
Chọn chiều dương là chiều chuyển động. Trọng lượng của xe P=mg =1500.10=150000 N chiếu lên trục Oy ta có \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{0}=m.a_y=0\Rightarrow P=N\) Ap luc của xe lên đường ray: N=P=150000N Lực ma sát trượt: Fmst=\(N.\mu=15000.0,45=6750\left(N\right)\) 3) Chọn chiều dương là chiều chuyển động. Trọng lượng của xe P=mg Ap luc của xe lên đường ray: N=P=m.g Từ khi hãm phanh xe chỉ chịu tác dụng của lực ma sát trượt nên theo định luật II Niutơn, gia tốc của xe là: a=\(-\dfrac{F_{ms}}{m}=-\dfrac{\mu.m.g}{m}=-\mu.g\)=−0,2.9,8=−1,96m/s^2 Gọi s là đường đi từ khi hãm phanh đến lúc dừng lại. \(S=\dfrac{v^2-v_0^2}{2a}=\dfrac{0-\left(\dfrac{36}{3,6}\right)^2}{2.\left(-1,96\right)}\approx25,5\left(m\right)\)

Chọn đáp án A
Phân tích các lực tác dụng lên cơ hệ như hình vẽ.
Áp dụng địn luật II Newton cho cơ hệ ta có:
Chiếu (1) theo chiều chuyển động của hệ vật ta được:
Lực căng của dây là:
T = P2 – m2a = m2(g – a)
= 0,3.(10 – 5,2) = 1,44 N.