Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Từ giả thiết ta có SO là trục của đường tròn ngoại tiếp tam giác ABC và SA=SB=a. Trong mặt phẳng (SAO), trung trực của cạnh SA cắt SO tại I thì I là tâm của mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được:
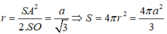

Đáp án: D
Hướng dẫn giải:
Gọi O là giao điểm của AC và BD, M là trung điểm của SA.
Qua M kẻ đường thẳng vuông góc với SA cắt SO tại I
⇒ I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
⇒ S I = R = 2
Ta có:
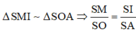
⇒ S O = S M . S A S I = S A 2 2 2
![]()
⇒ S A = S O 2
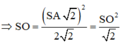
![]()
⇒ A B = 2 ⇒ S A B C D = A B 2 = 4
⇒ V S . A B C D = 1 3 . S O . S A B C D = 4 2 3

Đáp án A
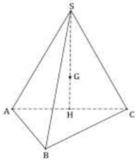
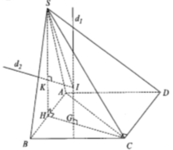
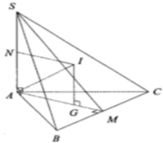
Do các cạnh bên cùng tạo với đáy một góc bằng nhau nên hình chiếu vuông góc của S trên mặt đáy trùng với tâm đường tròn ngoại tiếp tam giác ABC.
Mà tam giác ABC vuông tại B nên trung điểm H của AC chính là hình chiếu vuông góc của S trên
mặt đáy ⇒ S H ⊥ ( A B C )
Góc giữa SA và mặt đáy chính là góc giữa SA và AC hay góc SAC= 60 o Tam giác SAC đều ⇒ Trọng tâm G chính là tâm đường tròn ngoại tiếp tam giác SAC và G ∈ S H
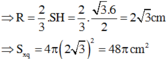

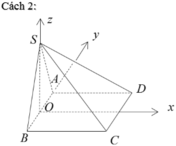
Chọn B
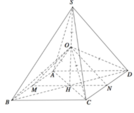
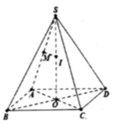
Gọi H là tâm mặt đáy, khi đó O thuộc SH.
Gọi M, N lần lượt là trung điểm các cạnh AB, CD. Ta có
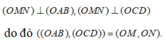

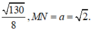
Do đó
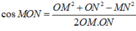

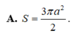
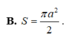
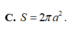

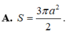
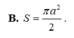

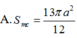
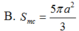
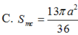
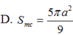

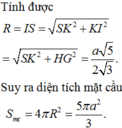
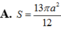
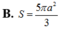

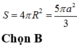


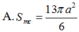

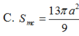
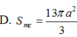

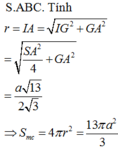
Đáp án D
Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp đó có đáy là một đa giác nội tiếp được đường tròn nên mệnh đề A và B đúng. Hình chps có các cạnh bên bằng nhau có hình chiếu vuông góc của đỉnh lên mặt đáy là tâm đường tròn ngoại tiếp đáy nên hình chóp đó có đáy nội tiếp được đường tròn và do đó đáp án C đúng.