Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
Vì x2 + 4 > 0 ∀x ∈ R nên A = ∅.
(x2 - 4)(x2 + 1) = 0 ⇔ (x2 - 4) = 0 ⇔ x = ±2 nên B = {-2; 2}.
|x| < 2 ⇔ -2 < x < 2 nên D = (-2; 2).
=> A ⊂ B = C ⊂ D.

Đáp án: D
(x2 - 4) (x2 - 1) = 0 ⇔ x = ±2; x = ±1 nên A = {-2; -1; 1; 2}
(x2 - 4) (x2 + 1) = 0 ⇔ x2 - 4 = 0 ⇔ x = ±2 nên B = {-2; 2}
x4 - 5x2 + 4)/x = 0 ⇔ x4 - 5x2 + 4 = 0 ⇔ x = ±2; x = ±1 nên D = {-2; -1; 1; 2}
=> A = D

Ta có tập nghiệm của phương trình là:
\(\left(x+2\right)\left(2x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\2x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Tập hợp S là:
\(S=\left\{-2;\dfrac{1}{2};3\right\}\)
Lần lược các phương án:
A. \(-2\in S\) (đúng)
B. \(3\in S\) (đúng)
C. \(2\in S\) (Sai)
D. \(\dfrac{1}{2}\in S\) (Đúng)
⇒ Chọn C

Đáp án C
Xét khẳng định C:
Nếu đường thẳng d đi qua gốc tọa độ O thì đường thẳng d có vectơ chỉ phương là OM → = (2; -1; 1)
Do u d → . n p → = 2.1 - 1.1 + 1.1 = 2 ≠ 0 nên đường thẳng d không song song với mặt phẳng (P)
(mâu thuẫn giả thiết)
Vậy khẳng định C là sai.

Các khẳng định là mệnh đề là:
a) \(3 + 2 > 5\)
d) \(1 - \sqrt 2 < 0\)
Các khẳng định là mệnh đề chứa biến là:
b) \(1 - 2x = 0\)
c) \(x - y = 2\)

a) Ta có: 8 > 4 nên để 8x > 4x thì x > 0
Do đó, chỉ đúng khi x > 0 (hay nói cách khác nếu x < 0 thì a sai)
b) Ta có: 4 < 8 nên để 4x > 8x thì x < 0 .
Do đó, khẳng định chỉ đúng khi x < 0
c) chỉ đúng khi x ≠ 0
d) Ta có: 8 > 4 nên với mọi x thì 8+ x > 4+ x ( tính chất cộng hai vế của BĐT với 1 số)
Do đó, khẳng định đúng với mọi x.
Vậy khẳng định d là đúng với mọi giá trị của x.
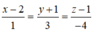
A, B, D đúng theo các tính chất của giá trị tuyệt đối, do đó C sai.
Đáp án: C