Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay x = -1, y = 3 vào đa thức, ta có giá trị của đa thức là:
(-1)2.32 + (-1).3 + (-1)3 + 33 = 32.
Chọn D

Khi x = - 1; y = 1 thì xy = (-1).1= -1
Ta có: xy – x2y2 + x3y3 – x4y4 + x5y5 – x6.y6
= xy – (xy)2 + (xy)3 – (xy)4 + (xy)5 – (xy)6
= -1 – (-1)2 + (-1)3 – (-1)4 + (-1)5 - (-1)6
= -1 – 1 + (-1) – 1 + (-1) – 1
= - 6
Chọn đáp án D

a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
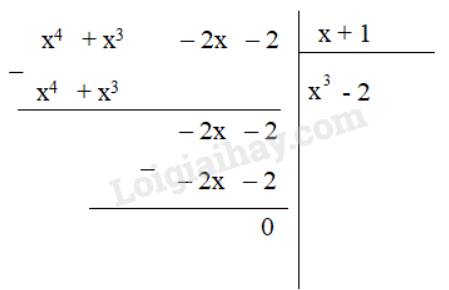
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
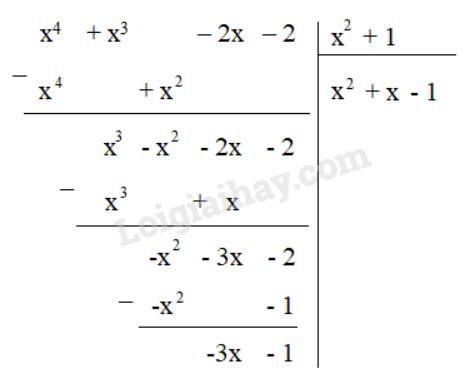
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn

Thay `x=-5`
`A. `
`5-(-5)=5+5=10`
`->` \(\text{x=-5 không phải là nghiệm của đa thức (k t/m)}\)
`B.`
`(-5)^3-25 = -125-25 = -150`
`->`\(\text{x=-5 không phải là nghiệm của đa thức (k t/m)}\)
`C.`
`(-5)+5=0`
`->`\(\text{x=-5 là nghiệm của đa thức (t/m)}\)
`D.`
`(-5)*(-5-5) = (-5)*(-25)=125`
`->`\(\text{x=-5 không phải là nghiệm của đa thức (k t/m)}\)
Xét các đáp án trên `-> C.`

a: \(F\left(x\right)=x^3+2x^2+3x+4\)
\(G\left(x\right)=x^3-x^2+3x+1\)
b: \(F\left(x\right)+G\left(x\right)=2x^3+x^2+6x+5\)
\(F\left(x\right)-G\left(x\right)=3x^2+3\)

a: \(C\left(x\right)=x^3+3x^2-x+6\)
\(D\left(x\right)=-x^3-2x^2+2x-6\)
b: Bậc của C(x) là 3
Hệ số tự do của D(x) là -6
c: \(C\left(2\right)=8+3\cdot4-2+6=20-2+6=24\)
d: \(C\left(x\right)+D\left(x\right)=x^2+x\)
a.
b. Bậc của C(x) là 3
Hệ số tự do của D(x) là -6
c.
d.

x3 – 5y2 + x + x3 – y2 – x
= (x3 + x3) – (5y2 + y2) + (x – x)
= (1+ 1).x3 – (5+1).y2 + (1- 1).x
= 2x3 – 6y2
Đáp án đúng là (C) 2x3 - 6y2

Lời giải:
a.
$P(x)=2x^4+(x^3-5x^3)+2x^2+(-2x+x)+1$
$=2x^4-4x^3+2x^2-x+1$
b)
$P(0)=2.0^4-4.0^3+2.0^2-0+1=1$
$P(1)=2-4+2-1+1=0$
c.
$P(1)=0$ (theo phần b) nên $x=1$ là nghiệm của đa thức $P(x)$
$P(-1)=2+4+2+1+1=10\neq 0$ nên $x=-1$ không là nghiệm của đa thức $P(x)$

Thay x = -1 vào biểu thức đã cho ta được:
(-1) + ( -1)3 + (-1)5 + (-1)7 +...+ (-1)101
= (-1) + (-1) + (-1) + (-1) +(- 1)+ ... + (-1) (51 số -1)
= -51.
Chọn đáp án C
Đa thức b là đa thức một biến.
Vì đa thức b có một biến duy nhất là \(x\), ba biến còn lại có hai biến là \(x\) và \(y\).
đa thức b là đa thức có một biến x còn 8 không phải là biến