Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
\(f\left(x\right)=\sqrt{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}}-\sqrt{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}=m\)
Tọa độ hóa bài toán bằng cách gọi \(A\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)\) và \(B\left(\frac{1}{2};\frac{\sqrt{3}}{2}\right)\) là hai điểm cố định trên mặt phẳng tọa độ Oxy, M là điểm di động có tọa độ \(M\left(x;0\right)\)
\(\Rightarrow AM=\left|\overrightarrow{AM}\right|=\sqrt{\left(x+\frac{1}{2}\right)^2+\left(0-\frac{\sqrt{3}}{2}\right)^2}=\sqrt{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}}\)
\(BM=\left|\overrightarrow{BM}\right|=\sqrt{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}\)
\(\Rightarrow f\left(x\right)=AM-BM\)
Mặt khác, theo BĐT tam giác ta luôn có
\(\left|AM-BM\right|< AB=\sqrt{\left(\frac{1}{2}+\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\right)^2}=1\)
\(\Rightarrow\left|f\left(x\right)\right|< 1\Rightarrow\left|m\right|< 1\Rightarrow-1< m< 1\)
Câu 2:
ĐKXĐ: \(1\le x\le3\)
Đặt \(\sqrt{x-1}+\sqrt{3-x}=a\ge0\)
Áp dụng BĐT Bunhiacốpxki:
\(\Rightarrow a\le\sqrt{\left(1+1\right)\left(x-1+3-x\right)}=2\sqrt{2}\)
Mặt khác
\(a^2=x-1+3-x+2\sqrt{\left(x-1\right)\left(3-x\right)}=2+2\sqrt{\left(x-1\right)\left(3-x\right)}\ge2\)
\(\Rightarrow2\le a\le3\)
Cũng từ trên ta có:
\(a^2=2+2\sqrt{\left(x-1\right)\left(3-x\right)}\Rightarrow\sqrt{\left(x-1\right)\left(3-x\right)}=\frac{a^2-2}{2}=\frac{1}{2}a^2-1\)
Phương trình trở thành:
\(a-\left(\frac{1}{2}a^2-1\right)=m\)
\(\Leftrightarrow-\frac{1}{2}a^2+a+1=m\)
Xét hàm \(f\left(a\right)=-\frac{1}{2}a^2+a+1\) trên \(\left[2;2\sqrt{2}\right]\)
\(f'\left(a\right)=-a+1< 0\) \(\forall a\in\left[2;2\sqrt{2}\right]\)
\(\Rightarrow f\left(a\right)\) nghịch biến trên \(\left[2;2\sqrt{2}\right]\)
\(\Rightarrow f\left(2\sqrt{2}\right)\le f\left(a\right)\le f\left(2\right)\Rightarrow-3+2\sqrt{2}\le f\left(a\right)\le1\)
Vậy:
- Nếu \(\left[{}\begin{matrix}m>1\\m< -3+2\sqrt{2}\end{matrix}\right.\) thì phương trình vô nghiệm
- Nếu \(-3+2\sqrt{2}\le m\le1\) pt có nghiệm

Căn bậc hai của một số thực dương a là một số thực b sao cho b 2 = a.
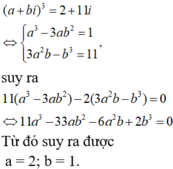
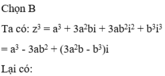
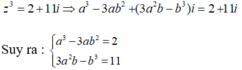



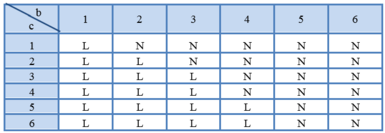

Chọn D.
Ta có: z = -121 nên z = (11i)2 .
Do đó z có hai căn bậc hai là z = 11i và z = -11i.