Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.

a) Nam có là một phần tử của tập hợp A
Ngân không là một phần tử của tập hợp B
b) \(A = \){Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
\(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó \(X \subset A\) và \(X \subset B\).

Ta có: \(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
và H = {Hương; Hiền; Hân}
Vậy các phần tử của H đều là phần tử của tập hợp B.

Tham khảo:
Ta có bảng sau:
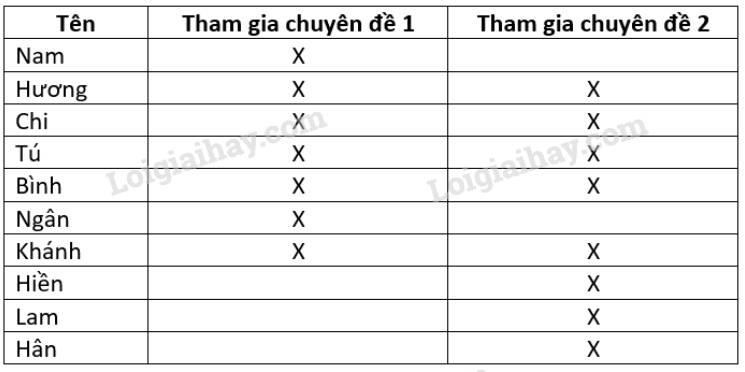
Dễ thấy: Có 10 bạn tham gia (1 chuyên đề hoặc cả hai)
Vậy có 2 thành viên vắng mặt trong cả hai chuyên đề.


a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: \(E = \{ {a_2};{a_7}\} \)
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: \(F = \{ {a_3};{a_4};{a_9}\} \)

a) Tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn là:
\(A = \{ {a_1};{a_2};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)
Tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ là:
\(B = \{ {a_1};{a_3};{a_5};{a_6};{a_8};{a_{10}}\} \)
b) Tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ là:
\(C = \{ {a_1};{a_5};{a_6};{a_8};{a_{10}}\} \)
c) Tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ là:
\(D = \{ {a_1};{a_2};{a_3};{a_5};{a_6};{a_7};{a_8};{a_{10}}\} \)

Chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức là một tổ hợp chập 2 của 22 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{22}^2\)( phần tử)
Gọi A là biến cố “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức”
Để chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức ta phải chọn 1 chuyên gia đến từ châu Á và 1 chuyên gia đến từ châu Âu. Có 10 cách chọn 1 chuyên gia đến từ châu Á và 12 cách chọn 1 chuyên gia đến từ châu Âu. Do đó, theo quy tắc nhân số phần tử của biến cố A là: \(n\left( A \right) = 10.12 = 120\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{120}}{{C_{22}^2}} = \frac{{40}}{{77}}\)

a) Chú ý rằng với hai người \(A\)và \(B\)thi đấu với nhau thì \(A\)thi đấu với \(B\)và \(B\)thi đấu với \(A\).
Mỗi người sẽ đấu với \(n-1\)người, nên tổng số ván đấu của giải là:
\(\frac{n\left(n-1\right)}{2}\).
b) Giả sử \(n=12\).
Tổng số ván đấu của giải là: \(\frac{12.11}{2}=66\).
Tổng số điểm của tất cả các kì thủ là: \(2\times66=132\).
Kì thủ cuối thắng ba kì thủ đứng đầu, do đó số điểm kì thủ cuối ít nhất là \(2.3=6\).
Do số điểm các kì thủ đôi một khác nhau nên tổng số điểm tối thiểu của tất cả các kì thủ là:
\(6+7+8+9+10+11+12+13+14+15+16+17=138>132\).
Do đó không thể xảy ra điều này.
Ta có đpcm.




A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}