Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nam có là một phần tử của tập hợp A
Ngân không là một phần tử của tập hợp B
b) \(A = \){Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
\(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}

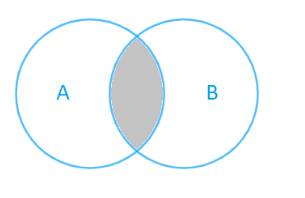
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó \(X \subset A\) và \(X \subset B\).

A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}

Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

Vì phần tử của A là số tự nhiên lớn hơn 8 và nhỏ hơn 14 nên 8 và 14 không thuộc tập hợp A. Vậy A = {9; 10; 11; 12; 13}. Dùng tính chất đặc trưng cho các phần tử A = {x ∈ N | 8 < x < 14}

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

x − m x + 1 = x − 2 x − 1 ⇔ x ≠ ± 1 m x = m + 2
Phương trình đã cho có nghiệm ⇒ m ≠ 0 x = 1 + 2 m ≠ ± 1 ⇔ m ≠ 0 m ≠ 1
Vì m ∈ Z, m ∈ [−3; 5] nên m ∈ S = {−3; −2; 1; 2; 3; 4; 5}.
Đáp án cần chọn là: D




Ta có: \(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
và H = {Hương; Hiền; Hân}
Vậy các phần tử của H đều là phần tử của tập hợp B.