Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: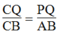 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra 
hay MN = PQ.
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: 
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: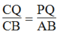 
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: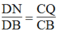 
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra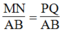 
hay MN = PQ.
Xét Tam giác ADB: MN // AB (gt)
Suy ra: DN/DB = MN/AB (Hệ quả định lí Talét) (1)
Xét Tam giác ACB: PQ // AB (gt)
Suy ra: CQ/CB = PQ/AB (Hệ quá định lí Talét) (2)
Ta có: NQ sog sog AB (gt)
AB sog sog CD (gt)
Suy ra: NQ sog sog CD (cùng sog sog AB)
Xét Tam giác BDC: NQ sog sog CD (cmt)
Suy ra: DN/DB = CQ/CB (Định lí Talét) (3)
Từ (1), (2) và (3) suy ra: MN/AB = PQ/AB
Suy ra: MN = PQ (đpcm).
a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ
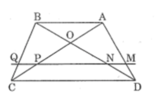
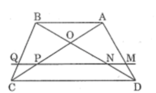
Sửa đề: Hình thang \(ABCD\left(BC//AD\right)\) Ý 2: \(MN//AD//BC\)
Hình tự vẽ nha <3
Gọi \(E,F\) lần lượt là trung điểm của các cạnh \(BC;AD\)
Gọi \(H\) là giao điểm của \(PE\) và \(AD\) và \(K\) là giao điểm của \(PK\) và \(BC\)
Xét \(\Delta MBE\) có: \(BE//AH\)
\(\Rightarrow\frac{MB}{MA}=\frac{BE}{HA}\)
Lại có: \(\frac{EC}{AH}=\frac{BE}{HA}\Rightarrow\frac{MB}{MA}=\frac{EC}{AH}\)
Chứng minh tương tự ta có: \(\frac{NC}{ND}=\frac{CK}{AF}\)
Xét \(\Delta PAH\) có: \(EC//AH\)
\(\Rightarrow\frac{PC}{PA}=\frac{EC}{AH}\)
Xét \(\Delta PAF\) có: \(CK//AF\)
\(\Rightarrow\frac{PC}{PA}=\frac{CK}{AF}\Rightarrow\frac{MB}{MA}=\frac{NC}{ND}\Rightarrow MN//AD//BC\left(đpcm\right)\)