Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cau1: gọi H là chân đường cao kẻ từ O đến đt (d) .\(\Rightarrow OH=2\)
giao điểm (d) và Oy la A(0,4) va giao diem (d) voi Ox la B(\(\dfrac{4}{1-m}\),0)
ta có \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
\(\Leftrightarrow\dfrac{1}{4}=\dfrac{1}{16}+\dfrac{\left(1-m\right)^2}{16}=\dfrac{1+\left(1-m\right)^2}{16}\)
\(\Rightarrow\left[{}\begin{matrix}1-m=\sqrt{3}\\1-m=-\sqrt{3}\end{matrix}\right.\Rightarrow m=1+\sqrt{3}\left(m>0\right)\)
cau2: goi \(\Delta\)là đường thẳng đi qua B(-5 ;20) vã C(7;-16) Pt \(\Delta\): y= ax+b
tọa độ B,C thõa mãn pt \(\Delta\)\(\left\{{}\begin{matrix}20=-5a+b\\-16=7a+b\end{matrix}\right.\Rightarrow a=-3;b=5\)
\(\Rightarrow\)y= -3x +5 (\(\Delta\)).để 3 điểm A ,B ,C thẳng hàng thi toa do A(\(\sqrt{x-1},-37\)).thoa pt\(\Delta\)
-37= -3\(\sqrt{x-1}+5\)\(\Leftrightarrow\sqrt{x-1}=14\)
\(\Rightarrow x=197\)

2mx -4m +10x -1 -y =0
2m(x-2) +(10x -1-y) =0
x =2 ; y =19 pt đúng với mọi m
=> h/s luôn qua điểm M(2;19) gọi K/c từ A đến d là AH
khoảng cách lờn nhất AH= AM ( AH </ AM)
khi đó AH vuông góc AM
+ gọi pt qua AM là y =ax +b => a =4 ; b =11
=>(2m+10) . 4 =-1
2m = -1/4 -10 =- 41/4
m =-41/8

b) Xét tam giác OMB vuông tại O có:
BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2
Tương tự tam giác OAB vuông tại O có:
B A 2 = O A 2 + O B 2 = 1 + 1 = 2 ⇒ BA = 2
Xét tam giác MAB có:
B M 2 + B A 2 = 2 + 2 = 4 = A M 2
⇒ ΔMAB vuông tại B
Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = 2

a: Để (d1) và (d2) cắt nhau thì \(2m+1\ne m+2\)
=>\(2m-m\ne2-1\)
=>\(m\ne1\)
b: Khi m=-1 thì (d1): \(y=\left(2-1\right)x+1=x+1\)
Khi m=-1 thì (d2): \(y=\left(1-2\right)x+2=-x+2\)
Vẽ đồ thị:
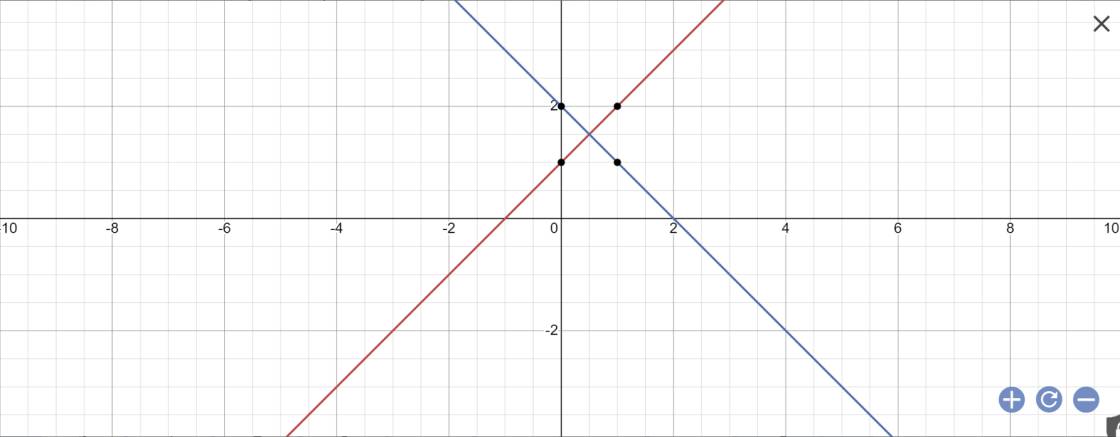
Phương trình hoành độ giao điểm là:
x+1=-x+2
=>x+x=2-1
=>2x=1
=>\(x=\dfrac{1}{2}\)
Thay x=1/2 vào y=x+1, ta được:
\(y=\dfrac{1}{2}+1=\dfrac{3}{2}\)
c:
(d1): y=(m+2)x+1
=>(m+2)x-y+1=0
Khoảng cách từ A(1;3) đến (d1) là:
\(d\left(A;\left(d1\right)\right)=\dfrac{\left|1\left(m+2\right)+3\cdot\left(-1\right)+1\right|}{\sqrt{\left(m+2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|m\right|}{\sqrt{\left(m+2\right)^2+1}}\)
Để d(A;(d1)) lớn nhất thì m+2=0
=>m=-2
Vậy: \(d\left(A;\left(d1\right)\right)_{max}=\dfrac{\left|-2\right|}{\sqrt{\left(-2+2\right)^2+1}}=\dfrac{2}{1}=2\)



PT giao Ox: \(x=\dfrac{3-4m}{2m-3}\Leftrightarrow A\left(\dfrac{3-4m}{2m-3};0\right)\Leftrightarrow OA=\left|\dfrac{3-4m}{2m-3}\right|\)
PT giao Oy: \(y=4m-3\Leftrightarrow B\left(0;4m-3\right)\Leftrightarrow OB=\left|4m-3\right|\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-3\right)^2}{\left(4m-3\right)^2}+\dfrac{1}{\left(4m-3\right)^2}\)
\(\Leftrightarrow\dfrac{1}{OH^2}=\dfrac{4m^2-12m+10}{\left(4m-3\right)^2}\\ \Leftrightarrow OH^2=\dfrac{16m^2-24m+9}{4m^2-12m+10}\)
Đặt \(OH^2=t\)
\(\Leftrightarrow4m^2t-12mt+10t=16m^2-24m+9\\ \Leftrightarrow m^2\left(4t-16\right)-m\left(12t-24\right)+10t-9=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm
\(\Leftrightarrow\Delta=\left(12t-24\right)^2-4\left(10t-9\right)\left(4t-16\right)\ge0\\ \Leftrightarrow144t^2-576t+576-160x^2+784x-576\ge0\\ \Leftrightarrow-t^2+13t\ge0\\ \Leftrightarrow0\le t\le13\\ \Leftrightarrow OH\le\sqrt{13}\)
Dấu \("="\Leftrightarrow\) PT có nghiệm kép hay \(m=\dfrac{12t-24}{8t-32}=\dfrac{3t-6}{2t-8}=\dfrac{39-6}{26-8}=\dfrac{33}{18}\)