Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

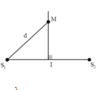
S1 S2 I M x
Giả sử S1S2 = 2d, điểm M cách trung điểm I một đoạn x có biên độ 1cm.
Bước sóng: \(\lambda=\frac{v}{f}=\frac{40}{20}=2cm\)
Giả sử sóng do S1 đến M lệch pha hơn sóng do S2 đến M là \(\varphi\), ta có: \(\varphi=\frac{4\pi x}{\lambda}\)
Biên độ của M là tổng hợp 2 dao động do S1 và S2 đến, ta có: \(6^2+8^2+2.6.8.\cos\varphi=1\Rightarrow\cos\varphi=\frac{-99}{96}<-1\), vô lí
Bạn xem lại xem đề bài có nhầm lẫn đâu không nhé.
Bạn làm sai rồi nhé, kia là mm và cm, đề này chuẩn
Đáp án 0,25 nhé baby ![]()

\(\lambda=\frac{v}{f}=\frac{30}{15}=2cm\)
Vì 2 nguồn cùng pha nên số điểm dao động với biên độ cực đại trên đoạn AB thỏa mãn:
\(-AB< k\lambda< AB\)
\(\Leftrightarrow\) -8,2 < 2k < 8,2
\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;^+_-4\)
Vậy có 9 điểm dao động với biên độ cực đại trên đoạn AB.
Số điểm dao động với biên độ cực tiểu trên đoạn AB thỏa mãn:
\(-AB< \left(k+0,5\right)\lambda< AB\)
\(\Leftrightarrow\) -8,2 < (k+0,5).2 < 8,2
\(\Leftrightarrow\) -4,6 < k < 3,6
\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;-4\)
Vậy có 8 điểm có biên độ dao động cực tiểu trên đoạn AB.

Đáp án: D
HD Giải: λ = 30 15 = 2cm
Số điểm dao động với biên độ cực đại, ta có:
-AB < kλ < AB
<=> -8,2 < 2k < 8,2
<=> - 4,1 < k < 4,1
Suy ra trên AB có 9 cực đại

Đáp án: A
HD Giải: λ = 80 2 π 100 π = 1,6cm
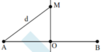
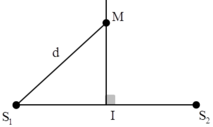
M cùng pha với nguồn A nên MA = d = (được rút ra từ phương trình sóng tại M với d1 = d2 = d)
Ta có điều kiện MA > AO = AB/2 nên
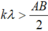
<=> 1,6k > 6
<=> k > 3,75
MA nhỏ nhất nên chọn k = 4
MA = 4.1,6 = 6,4 cm

Đáp án C
*Hai nguồn cùng pha nên những điểm dạo động nằm trên đường trung trực của AB (cách đều hai nguồn) đều dao động với biên độ cực đại A=2a= 10mm.

Đáp án A
+ Bước sóng của sóng λ = 2 π v ω = 8 m m
+ Điểm M trên trung trực của S1S2 dao động với phương trình u M = 2 a cos ( ω t - 2 π d λ )
Để M ngược pha với nguồn thì 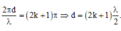
+ Mặt khác ![]()
Vậy d 1 = ( 8 . 2 + 1 ) λ 2 = 68 m m