Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
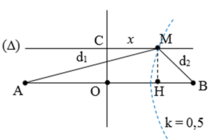
Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d2 và d1
Ta có ![]()
+ Điểm cực đại trên đoạn CD thỏa mãn:
![]() với
với
![]()
![]()
![]()
Có 7 giá trị của k là ![]() nên có 7 điểm cực đại trên CD.
nên có 7 điểm cực đại trên CD.
+ Điểm cực tiểu trên đoạn CD thỏa mãn
 ,
,
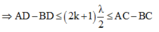
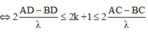
![]()
Có 6 giá trị của k thỏa mãn
![]() nên có 6 điểm cực tiểu trên CD.
nên có 6 điểm cực tiểu trên CD.

Đáp án B
- Xét trên tam giác vuông AOC có OA = 6 cm, OC = 8 cm → AC = 8 2 + 6 2 = 10cm.
- Gọi M là điểm nằm trên CO dao động cùng pha với nguồn → AM = kλ = 1,6k.
Lại có AO ≤ AM ≤ AC ↔ 6 ≤ 1,6k ≤ 10 → 3,75 ≤ k ≤ 6,75
Có 3 giá trị k nguyên thỏa mãn → Trên CO có 3 điểm dao động cùng pha với nguồn.
- Trên đoạn DO (với D đối xứng với C qua O) cũng có 3 điểm dao động cùng pha với nguồn.
→ Trên CD có tất cả có 6 điểm dao động cùng pha với nguồn.

Chọn đáp án B
Xét tam giác vuông AOC có OA = 6 cm và OC = 8 cm → AC =10 cm.
- Gọi M là điểm nằm trên đoạn CO và dao động cùng pha với nguồn → AM = kλ = 1,6k.
A O ≤ A M ≤ A C → 6 ≤ 1,6 k ≤ 10 → 3,75 ≤ k ≤ 6,75
Có 3 giá trị k nguyên thỏa mãn → có 3 điểm trên đoạn CO dao động cùng pha với nguồn.
- Tương tự trên đoạn DO cũng có 3 điểm dao động cùng pha với nguồn.
→ Có 6 điểm trên đoạn CD dao động cùng pha với nguồn.

Đáp án B
Xét tam giác vuông AOC có OA = 6 cm và OC = 8 cm → AC =10 cm.
- Gọi M là điểm nằm trên đoạn CO và dao động cùng pha với nguồn → AM = kλ = 1,6k.
A O ≤ A M ≤ A C → 6 ≤ 1 , 6 k ≤ 10 → 3 , 75 ≤ k ≤ 6 , 75
Có 3 giá trị k nguyên thỏa mãn → có 3 điểm trên đoạn CO dao động cùng pha với nguồn.
- Tương tự trên đoạn DO cũng có 3 điểm dao động cùng pha với nguồn.
→ Có 6 điểm trên đoạn CD dao động cùng pha với nguồn.

Đáp án A
+ Số dãy cực đại giao thoa - AB λ ≤ k ≤ A B λ ⇔ - 5 , 3 ≤ k ≤ 5 , 3
→ có 11 dãy.
+ Xét tỉ số: AD - BD λ = - 2 , 2
→ Trên BD có 7 cực đại dao thoa ứng với k = –1….5
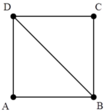

Đáp án A
+ Tần số góc của khung dây ω = 2 πn = 2 π . 50 = 100 π rad / s rad/s
→ Suất điện động cảm ứng cực đại
E 0 = ωNBS = 100 π . 500 . 2 5 π . 220 . 10 - 4 = 220 2 V .

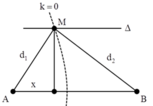
+ Để M là cực tiểu và gần trung trực của của AB nhất thì M phải nằm trên cực tiểu ứng với k = 0.
→ d2 – d1 = (0 + 0,5)λ = 1 cm.
Từ hình vẽ, ta có:
d 1 2 = 2 2 + x 2 d 2 2 = 2 2 + 8 − x 2 → 2 2 + 8 − x 2 − 2 2 + x 2 = 1
→ Giải phương trình trên ta thu được x = 3,44 cm.
Vậy khoảng cách ngắn nhất giữa M và trung trực AB là 4 – 3,44 = 0,56 cm.
Đáp án A

Số điểm dao động với biên độ cực tiểu trên CD thỏa mãn:
\(AD\leq d_1 \leq AC \Rightarrow -AC \leq -d_1\leq -AC\\ BC\leq d_2 \leq BD \\\)=> \(BC-AC\leq d_2-d_1\leq AC-AD\)
\(\Rightarrow 6-6\sqrt{2} \leq (k+0.5)\lambda\leq 6\sqrt{2}-6\\ \Rightarrow -4.64 \leq k \leq 3.64\\ \Rightarrow k = -4;-3;-2;-1;0;1;2;3.\)
Có 8 điểm dao động với biên độ cực tiểu.