Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

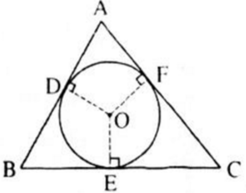
a, Tam giác ABC ngọi tiếp đường tròn \(\left(O\right)\)nên AB, BC, AC lần lượt là tiếp tuyến tại D, E , F của đường tròn.
Theo tính chất của hai đường tiếp tuyến cắt nhau, ta có:
AD = AF ; DB = BE ; FC = CE
Xét vế phải:
VP = AB + AC - BC
= ( AD + DB ) + ( AF + CF ) - ( BE + CE )
Thay DB = BE , FC = CE vào biểu thức trên, ta được:
VP = ( AD + BE ) + ( AF + CE ) - ( BE + CE )
= AD + BE + AF + CE - BE - CE
= ( AD + AF ) + ( BE - BE ) + ( CE - CE )
= AD + AF
= AD + AD = 2AD
Vậy 2AD = AB + AC - BC
b, Các hệ thức tương tự là:
2BD = BA + BC - AC
2CF = CA + CB - AB

A B C P F E N M x Q S O
Gọi S là giao điểm của 2 đường tròn (PCE) và (PBF).
Trước hết, ta thấy \(\Delta\)PCE ~ \(\Delta\)AOB => ^CPE = ^OAB. Tương tự: ^BPF = ^OAC.
Suy ra: ^CPE + ^BPF = ^OAB + ^OAC = ^BAC = 1800 - ^BPC => E,P,F thẳng hàng => ^EPS + ^FPS = 1800
Mà ^FPS + ^SNF = 1800 nên ^EPS = ^SNF => ^EMS = ^SNQ (Vì ^EPS = ^EMS)
=> Tứ giác SMQN nội tiếp. Hay S thuộc đường tròn (QMN).
Bằng các góc nội tiếp, ta có: ^BSC = ^BSP + ^CSP = ^BFP + ^CEP = ^BAC = const. Mà BC cố định
Nên S nằm trên đường tròn đối xứng với (O) và BC => Đường tròn (BCS) cố định
Ta sẽ chứng minh: Đường tròn (QMN) tiếp xúc với (BCS) cố định (tại điểm chung S).
Thật vậy, từ S vẽ tiếp tiếp Sx của đường tròn (QMN). Dễ thấy: ^MSx = ^MNS = ^PBS (Do tứ giác BPSN nội tiếp)
Xét đường tròn (PCE): ^MSC = ^MPC = ^CBP. Từ đó: MSx + ^MSC = ^PBS + ^CBP = ^CBS
Do đó: Sx cũng là tiếp tuyến của đường tròn (BCS). Cho nên (QMN) luôn tiếp xúc (BCS) cố định (đpcm).

đây là hình nhé, để cung cấp cho cách giải:

Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
B)
Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.

a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)
b) Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB

Tự vẽ hình nha
c) AE là tia phân giác của góc CAB => sđcEC=sđcEB=> EC=EB=> OE vuông góc vs BC
Góc OAE= góc OEA(1)
OE song song vs AH (cùng vuông góc vs BC)=> OEA=EAH(2)
Từ (1) và (2) => góc OAE= góc EAH => AE là tia phân giác của góc OAH

Cái này bạn chụp sách giải đúng ko ???
Sao cái này y chang như sách giải vậy ???

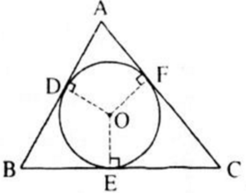

Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)