Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

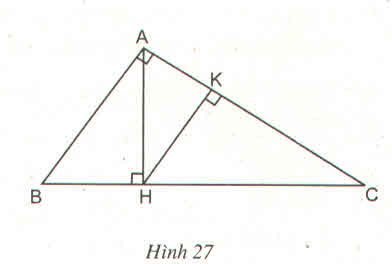
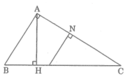
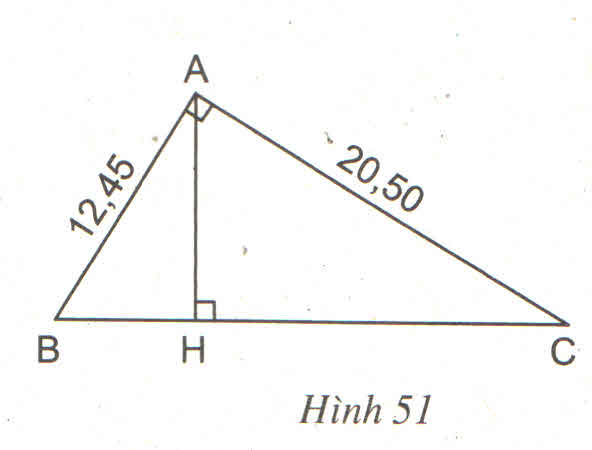
- △ ABC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
- △ ABC đồng dạng △ HAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ ABC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ∠ (HBA) = ∠ (HAC)
- △ HAB đồng dạng △ NCM
Hai tam giác vuông có góc nhọn ∠ (HAB) = ∠ (NCM)

Xét tứ giác ABED có:
AB//DE;AB=DE
=>ABED là hình bình hành ( một cặp cạnh vừa song song vừa bằng nhau)
nên AD=BE
Xét tam giác EDA và tam giác ABE có:
AB=DE (gt)
AE là cạnh chung
AD=BE ( vừa chứng minh)
=>tam giác EDA =tam giác ABE
<=>tam giác EDA đồng dạng với tam giác ABE (1)
Xét tứ giác ABCE có:
AB//EC;AB=EC
=>ABCE là hình bình hành (một cặp cạnh vừa song song vừa bằng nhau
=>AE=BC
Xét tam giác ABE và tam giác CEB có:
AB=EC(gt)
BE là cạnh chung
AE=BC (vừa chứng minh)
=>tam giác ABE=tam giác CEB
<=>tam giác ABE đồng dạng với tam giác CEB (2)
từ (1) và (2)
=>tam giác EDA đồng dạng với tam giác ABE và đồng dang với tam giác CEB.
Ai biết cách vẽ kí hiệu đồng dạng không chỉ mình cách vẽ với cảm mơn bạn nhiều.

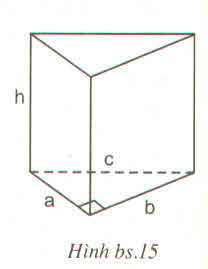
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| h | 8 | 18 | 17 | 24 | 13 |
| Diện tích 1 đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |
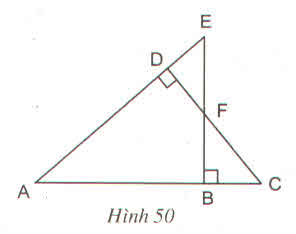


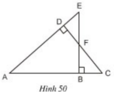





∆ADC ∽ ∆ABE vì góc A chung và \(\widehat{D}\)= \(\widehat{B}\) = 900
∆DEF ∆BCF vì \(\widehat{D}\) = \(\widehat{B}\) = 900 , \(\widehat{DEF}=\widehat{BFC}\)
∆DFE ∆BAE vì ( \(\widehat{D}=\widehat{B}\) = 900 , góc A chung)
∆BFC ∆DAC vì (\(\widehat{D}=\widehat{B}\) = 900, góc C chung)