Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

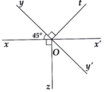
a) Vì Oy' là phân giác x ' O z ^ nên
x ' O y ' ^ = 1 2 x ' O z ^ = 1 2 . 90° = 45°
=> x O y ^ = x ' O y ' ^
Mà Ox và Ox' là hai tia đối nhau nên
x O y ^ và x ' O y ' ^ đối đỉnh
b) x ' O y ^ = 45°, y ' O t ^ = 90° => Ox' là phân giác t O y ' ^
Do đó x ' O t ^ = 45°
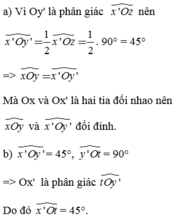
Sửa đề:
Trên đường thẳng x'x có 1 điểm O . Trên cùng một nửa mp bờ x'x vẽ hai tia Oy , Oz sao cho xOy = x'Oz = 120^o . Trên nửa mp đối của nửa mp chứa tia Oz , bờ x'x vẽ tia Oz' sao cho x'Oz' = 60^o a) Chứng tỏ 2 góc x'Oz' và xOz là 2 góc đối đỉnh b) Chứng tỏ Ox' là tia phân giác của yOz'
x x' z' y z O
a)Có tia Ox nằm giữa hai tia Oz và Oz'
=>\(\widehat{x'Oz}+\widehat{x'Oz'}=\widehat{zOz'}\)
Thay số:\(120^o+60^o=\widehat{zOz'}\)
=>\(\widehat{zOz'}=180^o\)
=> zz' là đường thẳng.
Có hai đường thẳng xx' và zz' cắt nhau ở O
=>\(\widehat{xOz}=\widehat{x'Oz'}\) (hai góc đối đỉnh)
b)Ta có:
+)\(\widehat{xOy}+\widehat{x'Oy}=180^o\)
+)\(\widehat{x'Oz}+\widehat{xOz}=180^o\)
Mà \(\widehat{xOy}=\widehat{x'Oz}\) (vì \(120^o=120^o\))
=>\(\widehat{x'Oy}=\widehat{xOz}\)
Lại có: \(\widehat{xOz}=\widehat{x'Oz'}\) (câu a)
=> \(\widehat{x'Oy}=\widehat{x'Oz'}\)
=>Ox' là tia phân giác của \(\widehat{yOz'}\)