Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
-gọi x là lượng cỏ mà 1 con bò ăn trong 1 tuần
- gọi y là lượng cỏ mọc lại trên 1arce/1 tuần
Ta có
- 12 con bò ăn trong 4 tuần: 12*4*x = 10/3 + 10/3*4y
- 21 con bò ăn trong 9 tuần: 21*9*x = 10 + 10*9*y
Giải hệ hai phương trình trên ta được: x=10/108 và y=1/12
Vậy a con bò ăn trong 18 tuần: a*18*x = 24 + 24*18*y
thay x, y vào ta tính được a=36
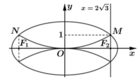
Diện tích Elip: 
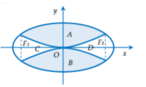
Chọn hệ trục tọa độ và gọi các điểm như hình.
Phương trình Elip là: 
Suy ra đường Elip nằm trên trục Ox là: 
Giao điểm của đường thẳng d:
x
=
2
3
đi qua tiêu điểm
F
2
và nửa Elip nằm bên trên trục Ox là 
Parabol đi qua các điểm 
có phương trình 
Khi đó diện tích 
Khi đó diện tích
Vậy số tiền cần chi phí: 
Chọn D.
Chọn C.
Phương pháp: Sử dụng tích phân để tính.
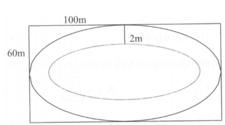
Cách giải: Vì hình có tính chất đối xứng nên ta tính phần diện tích ở góc
Phương trình đường elip ở nửa trên là 
Đáp án B.
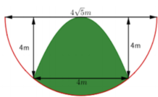
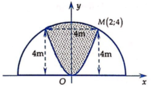Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là
y
=
R
2
-
x
2
=
2
5
2
-
x
2
=
20
-
x
2
.
Phương trình parabol (P) có đỉnh là gốc O sẽ có dạng y = a x 2 . Mặt khác (P) qua điểm M(2;4) do đó 4 = a . - 2 2 ⇔ a = 1 .
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn (phần tô màu) là S 1 = ∫ - 2 2 20 - x 2 - x 2 d x ≈ 11 , 94 ( m 2 ) .
Phần diện tích trồng cỏ là: S t r o n g c o = 1 2 S h i n h t r o n - S 1 ≈ 19 , 47592654 m 2 .
Vậy số tiền cần có là S t r o n g c o × 100000 ≈ 1948000 (đồng).
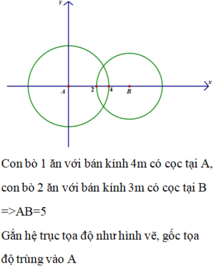
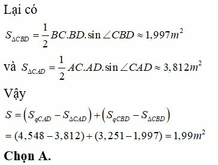
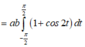
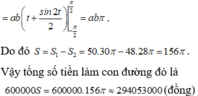
Đáp án A
Ta giải bằng phương pháp gắn hệ tọa độ Oxy, với gốc tọa độ O chính là chỗ cây cộc buộc con bò có sợi dây dài 3m, trục Ox là đường nối 2 cây cộc buộc dây của 2 con bò, ta được như hình vẽ.
Khi đó con bò có sợi dây 3m có thể ăn cỏ trong hình tròn giới hạn bởi đường tròn có bán kính 3m và có phương trình đường tròn tâm O là
là đường phía trên trục hoành. Ta cũng có phần cỏ của con bò có sợi dây 4m bị hạn chế trong đường tròn có phương trình tâm A, bán kính 4 là
Giao điểm của 2 đường tròn này là nghiệm của hệ 2 pt đường tròn đó
Ta chỉ cần tính phần diện tích phía trên trục hoành, phần dưới trục hoành có độ lớn cũng bằng như vậy. Từ B ta vẽ đường nét đứt vuông góc với Ox để chia đôi phần cần tính diện tích phía trên trục hoành, ta có