


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



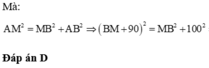

Chọn đáp án B
Đặt A B = l = 50 c m , bước sóng λ = v . T = 8 c m .
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
− l λ < k < l λ ⇒ − 6,25 < k < 6,25 ⇒ k = 0, ± 1,...., ± 6.
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒MA = MB + 48 (cm). MB⊥AB
⇒ M A 2 = A B 2 + M B 2 ⇔ ( M B + 48 ) 2 = A B 2 + M B 2 ⇔ M B 2 + 96 M B + 48 2 = 50 2 + M B 2 ⇔ M B = 50 2 − 48 2 96 = 2,04 c m

Đáp án B
Đặt AB =l = 50 cm, bước sóng λ = v.T = 8cm.
Khi hai nguồn dao động cùng pha,số vân có biên độ dao động cực đại bằng số giá trị của k thoả mãn
- 1 λ < k < 1 λ ⇒ - 6 , 25 < k < 6 , 25 ⇒ k = 0 , ± 1 , . . . , ± 6
→ Có 13 vân cực đại, vân chính giữa là vân cực đại bậc k = 0, vân cực đại gần B nhất là vân bậc 6. Điểm M trên đường Bx vuông góc với AB sóng có biên độ cực đại và M gần B nhất thì M là giao điểm của Bx và vân cực đại bậc 6, MA – MB = k.λ= 6.8 = 48 cm.
⇒ MA = MB + 48 (cm). MB⊥AB
⇒ MA 2 = AB 2 + MB 2 ⇔ ( MB + 48 ) 2 = AB 2 + MB 2 ⇔ MB 2 + 96 MB + 48 2 = 50 2 + MB 2 ⇔ MB = 50 2 - 48 2 96 = 2 , 04 cm

- Ta có:
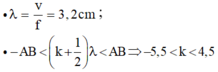
- Để điểm M dao động với biên độ cực tiểu gần B nhất thì:
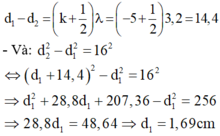
- Để điểm M dao động với biên độ cực tiểu xa B nhất thì:
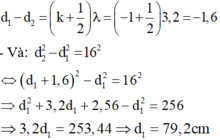

Đáp án D
λ = v f = 3 , 2
Ta có : -AB < k + 1 2 λ < A B
⇒ - 5 , 5 < k < 4 , 5
Để điểm M dao động với biên độ cực tiểu gần B nhất thì : d 1 - d 2 = k + 1 2 λ = - 5 + 1 2 3 , 2 = - 14 , 4
Và d 2 2 - d 1 2 = 16 2
⇔ ( d 1 + 14 , 4 ) 2 - d 1 2 = 16 2 ⇒ d 1 2 + 28 , 8 d 1 + 207 , 36 - d 1 2 = 256
⇒ 28 , 8 d 1 = 48 , 64 ⇒ d 1 = 1 , 69 cm

Chọn đáp án C
ta có lamda= 4cm. để MA min thì M phải thuộc cực tiểu xa đường trung trực nhất. xét -AB/4-1/2<= K <=
AB/4-1/2 => -4,75<= K <=3,75. => k= -4.
M thuộc cực tiểu nên MA-MB= (2k+1).lamda/2 <=>d1- căn( d1^2 + AB^2}= (2.-4 +1)2 <=>d1= 3,32