Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

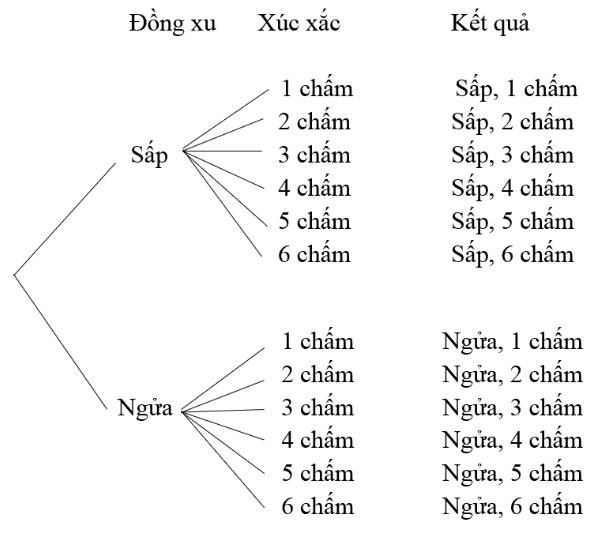
a) Kết quả của đồng xu và xúc xắc xảy ra đồng thời nên kết quả xảy ra gồm 2 kết quả liên tiếp nhau
Kết quả 1: Kết quả của đồng xu, có 2 kết quả: Sấp và ngửa
Kết quả 2: Kết quả của xúc xắc, có 6 kết quả: mỗi kết quả của mỗi mặt con xúc xắc
Áp dụng quy tắc nhân, ta có số kết quả có thẻ xuất hiện khi gieo đồng thời một đồng xu và một con xúc xắc là:
\(2.6 = 12\)
Vậy có 12 kết quả có thể xáy ra
b)

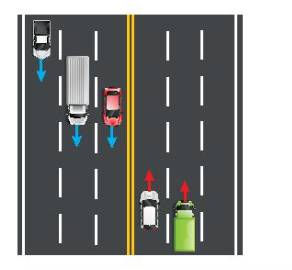
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

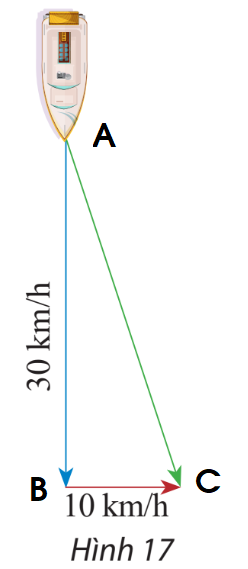
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

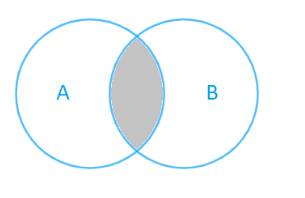
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A

Kết quả của mỗi lần thử là một cặp (i; j) với i và j lần lượt là số chấm xuất hiện trên hai xúc xắc, hai con xúc xắc gieo đồng thời nên không quan tâm thứ tự, ta có không gian mẫu là:
\(\Omega = \begin{array}{l}\{(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;2),(2;3),(2;4),(2;5),(2;6),(3;3),(3;4),(3;5),(3;6),\\(4;4),(4;5),(4;6),(5;5),(5;6),(6;6)\}\end{array} \)
Không gian mẫu gồm có 21 kết quả, tức là \(n\left( \Omega \right) = 21\)
a) Ta có tập hợp miêu tả biến cố A
\(A = \left\{ {(1;1),(2;2),(3;3),(4;4),(5;5),(6;6)} \right\} \Rightarrow n\left( A \right) = 6\)
Do đó, xác suất của biến cố A là: \(P\left( A \right) = \frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{21}} = \frac{2}{7}\)
b) Ta có tập hợp miêu tả biến cố B
\(B = \left\{ {(6;3),(5;4)} \right\} \Rightarrow n\left( B \right) = 2\)
Do đó, xác suất của biến cố B là: \(P\left( B \right) = \frac{{n(B)}}{{n(\Omega )}} = \frac{2}{{21}}\)

Trong toán học, mỗi cách xếp thứ tự đá luân lưu của 5 cầu thủ được gọi là hoán vị.

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)
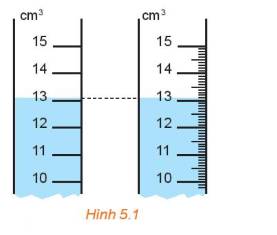






Giả sử ống nước thứ nhất là trang đo và ống nước thứ hai là Hòa đo.
Khi đó ống thứ nhất đo được là 13\(c{m^3}\), ống thứ hai là 13,1\(c{m^3}\)
Chú ý
Với ống thứ hai thì có vạch chia nhỏ hơn.