Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

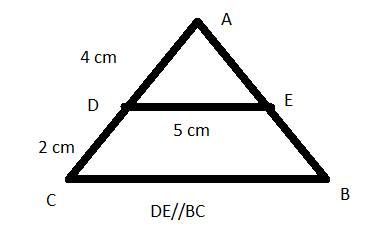
a) Ta có : AD + DB = AB ( vì D nằm trên cạnh AB)
=> AD + 2 = 8
=> AD = 6cm
Do đó : ADAB=68=34����=68=34
AEAC=912=34����=912=34
=> ADAB=AEAC=34����=����=34
b) Xét ΔADEΔ��� và ΔABCΔ��� có :
ˆA�^ chung
ADAB=AEAC����=����
=> ΔADE∽ΔABC(c.g.c)Δ���∽Δ���(�.�.�)
c) Vì IA�� là đường phân giác của ΔABCΔ��� nên
=> ABAC=IBIC=812=23����=����=812=23
Mà ADAB=AEAC����=���� (ΔADE∽ΔABC(cmt))(Δ���∽Δ���(���)) ⇒ABAC=ADAE=23⇒����=����=23
=>IBIC=ADAE⇒IB⋅AE=IC⋅AD(đpcm)����=����⇒��⋅��=��⋅��(đ���)


a: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{BM}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\left(1\right)\)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Ta có: M là trung điểm của BC
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
c: Xét ΔABC có
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC

Qua D kẻ đường thẳng song song với AB cắt AC tại E.
Dễ thấy tam giác AED vuông cân tại E nên \(\dfrac{AD}{\sqrt{2}}=AE=ED\).
Theo định lý Thales ta có: \(\dfrac{DE}{AB}=\dfrac{CE}{CA}=1-\dfrac{AE}{CA}=1-\dfrac{DE}{CA}\Rightarrow\dfrac{1}{DE}=\dfrac{1}{AB}+\dfrac{1}{AC}\Rightarrow\dfrac{\sqrt{2}}{AD}=\dfrac{1}{AB}+\dfrac{1}{AC}\).
Vậy ta có đpcm.

11C
12A
13C
15D
c.ơn bn nhiều