K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MT
20
NP
2
10 tháng 1 2016
Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.
NT
0
MN
16 tháng 2 2022
Tham khảo :
* Chứng minh:
a)
Ta có:
Tổng ba góc của tam giác \(ABC\) bằng \(180^o\) nên \(\widehat A + \widehat B = {180^o} - \widehat C\)
Góc \(ACx\) là góc ngoài của tam giác \(ABC\) nên\(\widehat {ACx}= 180^o-\widehat C\)
Do đó: \(\widehat {ACx} = \widehat A + \widehat B\).
b) Tam giác \(ABC\) vuông tại \(A\)
\( \Rightarrow \widehat A = {90^o}\)
Áp dụng định lí tổng các góc của một tam giác vào\(\Delta ABC\) ta có:
\(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A = {180^o} - {90^o} = {90^o}\)
c) Giả sử có tam giác \(ABC\) đều
\( AB = AC =BC \)
\( ΔABC\) cân tại \(A\) và cân tại \( B\).
\( \Rightarrow \widehat A = \widehat B;\,\,\,\,\widehat A = \widehat C\) (tính chất tam giác cân)
\( \Rightarrow \widehat A = \widehat B = \widehat C\)
d) Giả sử\(\Delta ABC\) có\(\widehat A = \widehat B = \widehat C\)
Có\(\widehat A = \widehat B\Rightarrow \)\(\Delta ABC\) cân tại \(C\), do đó \(CA=CB\).
Có\(\widehat B = \widehat C\Rightarrow \) \(\Delta ABC\) cân tại \(A\) do đó \(AC=AB\)
\( AB = AC = BC ΔABC\) là tam giác đều.
25 tháng 10 2023
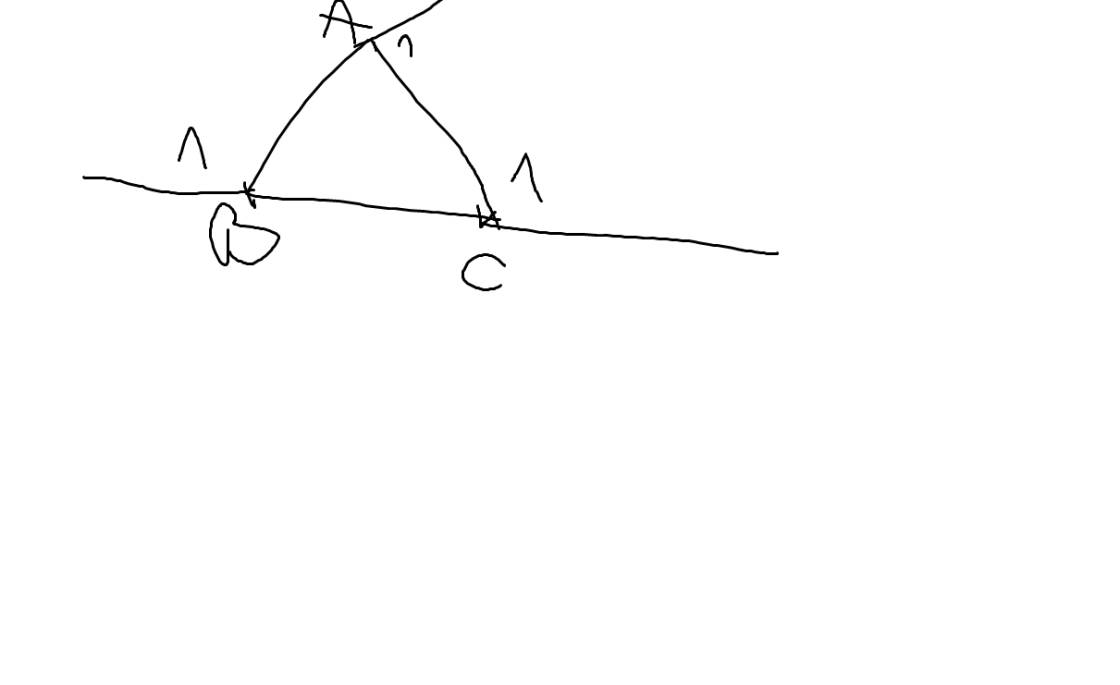
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)
NG
1
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$
Ta có tổng 3 góc trong của một tam giác là 180 .
Nên tổng các góc ngoài của một tam giác là 180 .