K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
22 tháng 9 2023
\(A=\dfrac{x+15}{x-2}=\dfrac{x-2+17}{x-2}\) \(\left(ĐK:x\ne2\right)\)
\(=\dfrac{x-2}{x-2}+\dfrac{17}{x-2}=1+\dfrac{17}{x-2}\)
Để \(A=1+\dfrac{17}{x-2}\in Z\)
thì \(\dfrac{17}{x-2}\in Z\)
\(\Rightarrow17⋮x-2\)
\(\Rightarrow x-2\inƯ\left(17\right)\)
\(\Rightarrow x-2\in\left\{1;17;-1;-17\right\}\)
\(\Rightarrow x\in\left\{3;19;1;-15\right\}\left(tm\right)\)
\(Vậy:x\in\left\{3;19;1;-15\right\}\)
KV
22 tháng 9 2023
Ta có:
x + 15 = x - 2 + 17
Để A ∈ Z thì (x + 15) ⋮ (x - 2)
⇒ 17 ⋮ (x - 2)
⇒ x - 2 ∈ Ư(17) = {-17; -1; 1; 17}
⇒ x ∈ {-15; 1; 3; 19}
ND
Nguyễn Đức Trí
VIP
23 tháng 9 2023
\(\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+...+\dfrac{1}{2019.2020}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{2019}-\dfrac{1}{2020}\)
\(=\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2019}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2020}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2019}+\dfrac{1}{2020}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2020}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2019}+\dfrac{1}{2020}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1010}\right)\)
\(=\dfrac{1}{1011}+\dfrac{1}{1012}+\dfrac{1}{1013}+...+\dfrac{1}{2020}\)
\(\Rightarrow dpcm\)
9 tháng 2 2018
ta có: \(\widehat{KAC}=\widehat{KCA}\) ( \(\Delta KAC\)cân tại \(K\))
\(\widehat{IAE}=\widehat{IEA}\) ( \(\Delta IAE\) cân tại \(I\))
\(\widehat{KBA}=\widehat{KAB}\) ( \(\Delta KBA\) cân tại \(K\) )
\(\widehat{IAE}=\widehat{KAB}\) ( cùng phụ với \(\widehat{KIA}\))
\(\Rightarrow\widehat{IEA}=\widehat{KBA}\)
xét \(\Delta KAE\)và \(\Delta ACB\) có:
\(\widehat{KAC}=\widehat{KCA}\)
\(\widehat{KBA}=\widehat{IEA}\)
\(\widehat{AKE}=\widehat{BAC}\) \(\left(=90^0\right)\)
\(\Rightarrow\Delta KAE=\Delta ACB\) ( G.G.G )
\(\Rightarrow AE=CB\)
\(KE=AB\)
\(AK=AC\)
b) theo câu a) \(AE=CB\)
xét trong \(\Delta DAE\) vuông có
\(AE\) là cạnh góc vuông
\(DE\) là cạnh huyền
\(\Rightarrow AE< DE\)
\(\Rightarrow DE>BC\)
LA
10 tháng 2 2018
Như mình đã hứa, giờ mk sẽ làm!
Xét\(\Delta AED\)vuông tại A có I là trung điểm ED
\(\Rightarrow AI=EI=ID\)
\(\Rightarrow\Delta AIE\)cân tại I
Tương tự, ta được \(\Delta AKC\) cân tại K
\(\Rightarrow\widehat{IAE}=\widehat{EIA};\widehat{KAC}=\widehat{C}\)
Mà \(\widehat{C}=\widehat{IEA}+\widehat{CKE}\)
\(\widehat{KAC}=\widehat{IAE}+\widehat{IAK}\)Do đó \(\widehat{IAK}=\widehat{CKE}\)
Gọi H giao điểm của AI và BC ta có
\(\widehat{HIK}+\widehat{HKI}=\widehat{AIK}+\widehat{IAK}=90^o\)
\(\Rightarrow AI\perp BC\)
b) Ta có: DE=2AI; BC=2AK
Mà \(AI\ge AK\), do đó \(DE\ge BC\)
12 tháng 2 2018
Sắp phải ăn cơm nên không có thời gian để vẽ hình bạn tự vẽ lấy nhé :3
Kẻ DH // AB
\(\widehat{DHB}=\widehat{ACB}\)( đồng vị )
Mà \(\widehat{ABC}=\widehat{ACB}\left(gt\right)\)
\(\Rightarrow\)\(\widehat{ABC}=\widehat{DHB}\)\(\Rightarrow\)\(\Delta DHB\)cân
\(\Rightarrow\)\(DH=DB\) ( 1 )
Xét tam giác CEI và tam giác IDH ta có ;
\(CE=DH\)
\(EI=ID\left(gt\right)\)
\(\widehat{CEI}=\widehat{IDH}\)
\(\Rightarrow\)\(\Delta CEI=\Delta IDH\left(c-g-c\right)\)
\(\Rightarrow\)\(\widehat{CIE}=\widehat{DIH}\)
Mà \(\widehat{CIE}+\widehat{CID}=180\)độ
\(\Rightarrow\)\(\widehat{DIH}+\widehat{CID}=180\)độ
\(\Rightarrow\)B ; I ; C thẳng hàng
Vậy B ; I ; C thẳng hàng ( ĐPCM )
A
12 tháng 2 2018
Vẽ DG // BC và cắt AC tại G
Do DG // BC nên tứ giác DGCB là hình thang ( đáy DG // BC), mà tam giác ABC cân tại A => góc B = C => DGBC là hình thang cân ( đáy DG // BC) => DB = GC ( tính chất
của hình thang cân)
Mà DB = CE => GC = CE và C thuộc GE => C là tđ của GE
Xét tam giác DGE có: C là tđ GE ; CF // DG ( Do DG // BC mà CF thuộc BC) => CF là đg trung bình ứng vs đáy DG của tam giác DGE => F là trung điểm của DE
DK
1
7 tháng 1 2021
Ta có: \(\dfrac{66666\cdot87654-33333}{22222\cdot87650-77777}\)
\(=\dfrac{33333\left(2\cdot87654-1\right)}{11111\left(2\cdot87650-7\right)}\)
\(=\dfrac{3\cdot175307}{175293}=\dfrac{525921}{175293}=\dfrac{175307}{58431}\)
9 tháng 10 2015
bạn có thể mua sách nâng cao hoặc là lên trang có nhiều dạng toán hay lắm nha.Mk ngồi chờ mãi còn chưa mua dc cuốn sách toán cho thằng em nak
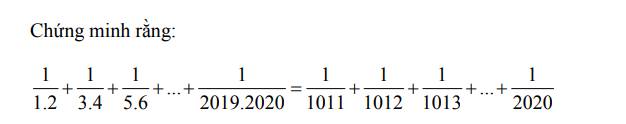
Ta có:
\(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+...+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(B=2008+\dfrac{2007}{2}+\dfrac{2006}{3}+...+\dfrac{1}{2008}\)
\(B=1+\left(\dfrac{2007}{2}+1\right)+\left(\dfrac{2006}{3}+1\right)+...+\left(\dfrac{2}{2007}+1\right)+\left(\dfrac{1}{2008}+1\right)\)
\(B=1+\dfrac{2009}{2}+\dfrac{2009}{3}+\dfrac{2009}{4}+...+\dfrac{2009}{2008}\)
\(B=2009\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{2009}\right)\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2009}}{2009\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2009}\right)}\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{1}{2009}\)
Tính tỉ số
, biết: