Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Bài 1 e bấm máy
Nhấn Shift + log sẽ xuất hiện tổng sigma
e nhập như sau:
x = 1
cái ô trống ở trên nhập 2007
còn cái biểu thức trong dấu ngoặc đơn là \(\left(\frac{1}{\left(X+1\right)\sqrt{X}+X\sqrt{X+1}}\right)\)
Rồi bấm "="
Chờ máy hiện kq sẽ hơi lâu :)
kq: 0.9776839079
2.
-B1: Tìm số dư của \(2^{2009}\) cho 11 đc kq là 6
- B2: Tìm số dư của \(3^6\) cho 11 đc kq là 3
Vậy \(3^{2^{2009}}\) chia 11 dư 3
3. Gọi độ dài đường chéo ngắn hơn là x, thì độ dài đường chéo kia là 3/2 x
Cạnh hình thoi: 37 : 4 = 9.25 (cm)
Theo định lý Pytago
\(x^2+\left(\frac{3}{2}x\right)^2=9.25^2\)
Vào Shift Solve giải ra tìm đc \(x\approx5.130976815\)
Vậy \(S=\frac{1}{2}x.\frac{3}{2}x=\frac{4107}{208}\approx19.7451923076\left(cm^2\right)\)

Lời giải:
Gọi chiều dài và chiều rộng hình chữ nhật lần lượt là $a$ và $b$ (m)
Độ dài đường chéo: $17=\sqrt{a^2+b^2}$ (theo định lý Pitago)
$\Leftrightarrow a^2+b^2=289(1)$
Diện tích hình chữ nhật: $ab=120$
Ta đi giải hpt \(\left\{\begin{matrix} a^2+b^2=289\\ ab=120\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (a+b)^2-2ab=289\\ ab=120\end{matrix}\right.\)
$\Rightarrow (a+b)^2=289+2ab=289+2.120=529$
$\Rightarrow a+b=23$
Chu vi hình chữ nhật: $2(a+b)=46$ (m)

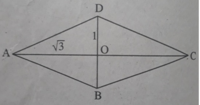
Coi đường chéo AC = 2 3 , đường chéo BD = 2 thì để ý rằng AC và BD vuông góc, ta có
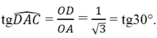
Nên ∠ (DAC) = 30 ° từ đó góc A của hình thoi là 60 ° . Suy ra ∠ C = 60 ° còn ∠ B = ∠ D = 120 °