Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số chiếc xe Wave là x (0 < x < 28, x ∈ N*)
Gọi số chiếc xe SH là y (0 < y < 28, y ∈ N*)Vì có tổng cộng 28 chiếc xe nên ta có phương trình: x + y = 28 (1)Vì nếu chủ cửa hàng bán hết 28 chiếc xe sẽ có 828 triệu đồng nên ta có phương trình:15x + 117y = 828 (2)Kết hợp hai phương trình (1) và (2), ta có hệ phương trình: x + y = 28 15x + 117y = 828Giải hệ trên ta được: x = 24 (TM), y = 4 (TM).Vậy cửa hàng có 24 chiếc xe Wave, có 4 chiếc xe SH.

Gọi số xe máy wave a và sh lần lượt là x; y ( x, y \(\in\)N* ; triệu đồng )
Ta có: x + y = 28 (1)
Giá của x chiếc xe wave a là: 15x ( triệu đồng )
Giá của y chiếc xe sh là: 117y ( triệu đồng )
Theo bài ra ta có: 15x + 117y = 828 (2)
Từ (1) và (2) ta có hệ: \(\hept{\begin{cases}x+y=28\\15x+117y=828\end{cases}}\)
Giải ra ta có x = 24 và y = 4 ( thỏa mãn )
Vậy ...

Gọi số tiền cho loại hàng 1 là x
số tiền cho loại hàng 2 là y ( x ; y thuộc N* )
Theo đề bài ta có : ( x + 8%x ) + ( y + 10%y ) = 2 730 000đ
<=> ( x + 2/25x ) + ( y + 1/10y ) = 2 730 000đ
<=> x( 1 + 2/25 ) + y( 1 + 1/10 ) = 2 730 000đ
<=> 27/25x + 11/10y = 2 730 000đ ( 1 )
Nếu thuế là 9% cho cả hai loại mặt hàng thì người đó phải trả 2 725 000đ
=> ( x + 9%x ) + ( y + 9%y ) = 2 725 000đ
<=> ( x + 9/100x ) + ( y + 9/100y ) = 2 725 000đ
<=> x( 1 + 9/100 ) + y( 1 + 9/100 ) = 2 725 000đ
<=> 109/100x + 109/100y = 2 725 000đ
<=> 109/100( x + y ) = 2 725 000đ
<=> x + y = 2 500 000đ ( 2 )
Từ (1) và (2) => Ta có hệ phương trình :
\(\hept{\begin{cases}\frac{27}{25}x+\frac{11}{10}y=2730000\\x+y=2500000\end{cases}}\)
Nhân 25/27 vào từng vế của (2)
\(\Rightarrow\hept{\begin{cases}\frac{27}{25}x+\frac{11}{10}y=2730000\\\frac{27}{25}x+\frac{27}{25}y=2700000\left(3\right)\end{cases}}\)
Trừ (1) cho (3) theo vế
\(\Rightarrow\frac{1}{50}y=30000\Rightarrow y=1500000\)
Thế y = 1 500 000 vào (2)
\(\Rightarrow x+1500000=2500000\Rightarrow x=1000000\)
Cả hai giá trị đều tmđk
Vậy người đó phải trả 1 000 000đ cho loại hàng 1
1 500 000đ cho loại hàng 2 ( không kể thuế nhập )

Gọi số xe mô tô và xe ô tô lần lượt là x,y
Theo đề, ta có: x+y=20 và 2x+4y=60
=>x=10 và y=10

Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y
(x, y > 0, triệu đồng; x < 2,17, y < 2,17)
Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x
+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.
Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)
Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x
+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.
Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:
1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)
Từ (1) và (2) ta có hệ phương trình :
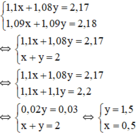
Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y
(x, y > 0, triệu đồng; x < 2,17, y < 2,17)
Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x
+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.
Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)
Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :
+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x
+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.
Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:
1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)
Từ (1) và (2) ta có hệ phương trình :
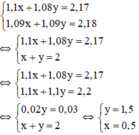
Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .

Giả sử không kể thuế VAT, người đó phải trả x triệu đồng cho loại hàng thứ nhất, y triệu đồng cho loại hàng thứ hai. Khi đó số tiền phải trả cho loại hàng thứ nhất, (kể cả thuế VAT 10%) là triệu đồng, cho loại hàng thứ hai, với thuế VAT 8% là
triệu đồng. Ta có phương trình
+
= 2,17 hay 1,1x + 1,08y = 2,17
Khi thuế VAT là 9% cho cả hai loại hàng thì số tiền phải trả là: = 2,18
hay 1,09x + 1,09y = 2,18.
Ta có hệ phương trình:
Giải ra ta được: x = 0,5; y = 1,5
Vậy loại thứ nhất 0,5 triệu đồng, loại thứ hai 1,5 triều đồng.
Ai giải thích hộ em tại sao chỗ kia lại là và
được không ạ ? Em không hiểu lắm
Gọi số xe loại một là: \(x\) (chiếc); (\(x\) \(\in\)N*)
Khi đó số xe loại hai là: 50 - \(x\) (chiếc)
Số tiền mua xe loại một là: \(x\) \(\times\) 2 = 2\(x\) ( triệu đồng)
Số tiền mua xe loại hai là: (50 - \(x\)) \(\times\) 6 = 300 - 6\(x\) (triệu đồng)
Theo bài ra ta có phương trình: 2\(x\) + 300 - 6\(x\) = 160
300 - 4\(x\) = 160
4\(x\) = 300 - 160
4\(x\) = 140
\(x\) = 140 : 4
\(x\) = 35
Vậy số xe loại một là 35 chiếc
Số xe loại hai là: 50 - 35 = 15 (chiếc)
Kết luận: Cửa hàng đã nhập 35 chiếc xe loại 1 và 15 chiếc xe loại 2