Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1,\sqrt{\left(2+\sqrt{7}\right)^2-\sqrt{\left(2-\sqrt{7}\right)^2}}\) ( áp dụng hđt thứ 3 \(a^2-b^2=\left(a-b\right)\left(a+b\right)\))
\(=\sqrt{\left(2+\sqrt{7}+2-\sqrt{7}\right)\left(2+\sqrt{7}-2+\sqrt{7}\right)}\)
\(=\sqrt{4\cdot\sqrt{7}}\)
\(2,\sqrt{\left(3\sqrt{5}-5\sqrt{2}\right)^2}-\sqrt{\left(5\sqrt{2}+3\sqrt{5}\right)^2}\)
\(\Leftrightarrow\sqrt{\left(3\sqrt{5}-5\sqrt{2}\right)^2}=\sqrt{\left(5\sqrt{2}+3\sqrt{5}\right)^2}\)
\(\Leftrightarrow\left(3\sqrt{5}-5\sqrt{2}\right)^2=\left(5\sqrt{2}+3\sqrt{5}\right)^2\)
\(\Leftrightarrow\left(3\sqrt{5}-5\sqrt{2}\right)^2-\left(5\sqrt{2}+3\sqrt{5}\right)^2\)
\(=\left(3\sqrt{5}-5\sqrt{2}+5\sqrt{2}+3\sqrt{5}\right)\left(3\sqrt{5}-5\sqrt{2}-5\sqrt{2}-3\sqrt{5}\right)\)
\(=6\sqrt{5}\cdot\left(-10\sqrt{2}\right)\)
\(3,\sqrt{10+2\sqrt{21}}-\sqrt{10-2\sqrt{21}}\)
\(\Leftrightarrow\sqrt{10+2\sqrt{21}}=\sqrt{10-2\sqrt{21}}\)
\(\Leftrightarrow10+2\sqrt{21}=10-2\sqrt{21}\)
\(\Leftrightarrow4\sqrt{21}\)
cuối lười tính nên thôi nhá :>

\(A=\sqrt{24+8\sqrt{5}}+\sqrt{7-4\sqrt{3}}\)
\(=\sqrt{5+2.4\sqrt{5}+16}+\sqrt{4-2.2\sqrt{3}+3}\)
\(=\sqrt{\left(\sqrt{5}+4\right)}^2+\sqrt{\left(2-\sqrt{3}\right)}^2\)
\(=|\sqrt{5}+4|+|2-\sqrt{3}|\)
\(=\sqrt{5}+4+4-\sqrt{3}\)
\(=\sqrt{5}-\sqrt{3}+8\)
Ko biết đề sai ko?

1. hiểu rồi k ngày đăng cầu mới--->trả lời ngay
2. chưa hiểu hỏi bải ngày--> nhận lời giải thích luôn
3.chưa k quay về câu 1

Vậy cái điều kiện \(x\ne\sqrt{3}\)người ta cho chi bạn. Bạn nên để ý là cái điều kiện người ta cho là nhằm cho cái đó nó xác định chớ không cho tào lao đâu. x # 0 cũng là vì lý do đó nên mình chắc cái đề trong sách in sai
Với điều kiện kèm theo thì mình chắc rằng cái đề phải là x - \(\sqrt{27}\) chứ không thể lad x - 27 được. Bạn xem lại đề nhé
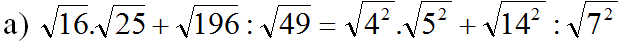
\(\left(2+1+3.\sqrt[3]{2}\left(\sqrt[3]{2}+1\right)\right)\left(\sqrt[3]{2}-1\right)\)
=\(\left(3+3\sqrt[3]{4}+3\sqrt[3]{2}\right)\left(\sqrt[3]{2}-1\right)\)
=\(3\sqrt[3]{2}+6+3\sqrt[3]{4}-3-3\sqrt[3]{4}-3\sqrt[3]{2}\)
=3