
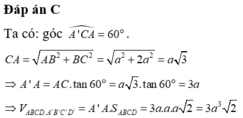
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

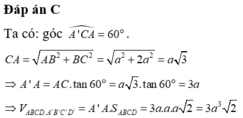

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

ღᏠᎮღĐiền❤RaiBo༻꧂
Phải giải chi tiết ra chứ, bài dễ mak, lớp 6 cx lm đc

Xem hình cho dễ trả lời nè https://kenh14cdn.com/thumb_w/620/2018/8/31/photo-1-15356853370631011068279.jpg

mk nhầm câu c là 25f(x)
câu d là 24f(x)
mk nhầm nũa câu hỏi là cái f(x+2)-f(x) là bỏ nha

Xét tam giác \(PBC\)và tam giác \(PAB\)có:
\(\frac{PB}{PA}=\frac{BC}{AB}=\frac{PC}{PB}=\sqrt{2}\)
suy ra \(\Delta PBC~\Delta PAB\left(c.c.c\right)\)
suy ra \(\widehat{PBC}=\widehat{PAB}\).
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}\)
\(=180^o-45^o-135^o\)

Lời giải:
b/ $x^2-4x+20=0$
$\Leftrightarrow (x-2)^2+16=0\Leftrightarrow (x-2)^2=-16< 0$ (vô lý)
Do đó pt vô nghiệm.
c/ $2x^3-3x+1=0$
$\Leftrightarrow 2x^2(x-1)+2x(x-1)-(x-1)=0$
$\Leftrightarrow (x-1)(2x^2+2x-1)=0$
$\Rightarrow x-1=0$ hoặc $2x^2+2x-1=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{-1\pm \sqrt{3}}{2}$