Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

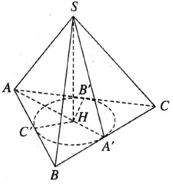
Kẻ SH ⊥ (ABC) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có SA′ ⊥ BC, SB′ ⊥ CA, SC′ ⊥ AB
Từ đó suy ra ∠ SA′H = ∠ SB′H = ∠ SC′H = 60 ° .
Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.
Do đó, AA ' 2 = AB 2 - BA ' 2 = 25 a 2 - 9 a 2 = 16 a 2
Vậy AA’ = 4a
Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.
Khi đó SABC = 6a.4a/2 = 12a2 = pr = 8ar
Từ đó suy ra r = 3a/2
Do đó
![]()
Thể tích khối chóp là:
![]()

Có: (SC, (ABCD)) = ∠SCB
Gọi: \(O=AC\cap BD\)
Có: \(OC=\dfrac{1}{2}AC=\dfrac{3}{2}a\)
\(OB=\dfrac{1}{2}BD=\dfrac{5}{2}a\)
Xét tam giác OBC vuông tại O (Do: ABCD là hình thoi nên AC ⊥ BD), có:
\(BC=\sqrt{OB^2+OC^2}=\dfrac{a\sqrt{34}}{2}\)
Xét tam giác SBC vuông tại B (Do: SB ⊥ (ABCD) ), có:
\(SB=BC.tan60^o=\dfrac{a\sqrt{102}}{2}\)
\(\Rightarrow V_{SABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{102}}{2}.\dfrac{1}{2}.3a.5a=\dfrac{5a^3\sqrt{102}}{4}\left(đvtt\right)\)