Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có 2 góc A và B bù nhau
=> \(\widehat{A}+\widehat{B}=180^o\)
Áp dụng dãy tỉ số bằng nhau , ta có :
\(\frac{A}{5}=\frac{B}{4}=\frac{A+B}{9}=\frac{180}{9}=20\)
=> \(\widehat{A}=20.5=100
;\widehat{B}=20.4=80\)

Ta có: \(2\widehat{A}-3\widehat{B}=20^0\) => \(2\widehat{A}=3\widehat{B}+20^0\)(1)
A và B là 2 góc bù nhau nên: \(\widehat{A}+\widehat{B}=180^0\) <=> \(2\widehat{A}+2\widehat{B}=360^0\). Thay (1) vào ta được:
\(3\widehat{B}+2\widehat{B}=360^0\) <=> \(5\widehat{B}=360^0\) => \(\widehat{B}=360:5=72^0\)
\(\widehat{A}=180-72=108^0\)
À mình nhầm đấy;
3B+20+2B=360
<=> 5B=340 => B=340:5=680
A=180-68=1120

a. Vì \(\widehat{xOy}\)= 600
\(\widehat{yOz}\)=900
nên \(\widehat{xOy}\)< \(\widehat{yOz}\)(vì 60<90)
=> Tia oy nằm giữa 2 tia Ox và Oz
vì tia oy nằm giữa 2 tia Ox và Oz
nên \(\widehat{yOz}\)+ \(\widehat{xOy}\)= \(\widehat{xOz}\)
900 + 600 = \(\widehat{xOz}\)
\(\widehat{xOz}\) = 1500
b. Số đo của góc bù với góc xOy là 1200
k mk nha thư

a) Ta có: \(\widehat{AOB}\) và \(\widehat{BOC}\) là hai góc kề bù(gt)
nên \(\widehat{AOB}+\widehat{BOC}=180^0\)
\(\Leftrightarrow\widehat{AOB}+5\cdot\widehat{AOB}=180^0\)
\(\Leftrightarrow6\cdot\widehat{AOB}=180^0\)
hay \(\widehat{AOB}=30^0\)
Ta có: \(\widehat{BOC}=5\cdot\widehat{AOB}\)(gt)
nên \(\widehat{BOC}=5\cdot30^0\)
hay \(\widehat{BOC}=150^0\)
Vậy: \(\widehat{AOB}=30^0\); \(\widehat{BOC}=150^0\)
b) Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{DOB}< \widehat{BOC}\left(75^0< 150^0\right)\)
nên tia OD nằm giữa hai tia OB và OC
\(\Leftrightarrow\widehat{COD}+\widehat{BOD}=\widehat{COB}\)
\(\Leftrightarrow\widehat{COD}=\widehat{COB}-\widehat{BOD}=150^0-75^0=75^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{COD}< \widehat{COA}\left(75^0< 180^0\right)\) nên tia OD nằm giữa hai tia OC và OA
\(\Leftrightarrow\widehat{COD}+\widehat{AOD}=\widehat{COA}\)
\(\Leftrightarrow\widehat{AOD}=\widehat{COA}-\widehat{COD}=180^0-75^0\)
hay \(\widehat{AOD}=105^0\)
Vậy: \(\widehat{AOD}=105^0\)
a) \(\widehat{AOB}\) và \(\widehat{BOC}\) kề bù \(\Rightarrow\widehat{AOB}+\widehat{BOC}=180^0\) mà \(\widehat{BOC}=5\widehat{AOB}\)
\(\Rightarrow\widehat{AOB}+5\widehat{AOB}=180^0\Rightarrow6\widehat{AOB}=180^0\\ \Rightarrow\widehat{AOB}=30^0\Rightarrow\widehat{BOC}=150^0\).
b) Do \(OD\) nằm trong góc \(\widehat{BOC}\) \(\Rightarrow\) tia \(OD\) nằm giữa hai tia \(OB,OC\)
\(\Rightarrow\)tia \(OB\) và tia \(OA\) nằm cùng phía nhau so với tia \(OD\)
\(\Rightarrow\) tia \(OB\) nằm giữa hai tia \(OA,OD\)
\(\Rightarrow\widehat{AOD}=\widehat{AOB}+\widehat{BOD}=30^0+75^0=105^0\).
c) Nếu chỉ xét trường hợp các góc tạo bởi hai tia liên tiếp nhau:
Trên nửa mặt phẳng bờ \(AC\) có \(n+4\) tia (gồm \(4\) tia \(OA,OB,OC,OD\) và \(n\) tia vẽ thêm).
Cứ hai tia cạnh nhau tạo thành 1 góc
\(\Rightarrow\) Ta có \(n+3\) góc.

Vì \(\widehat{A}\)và \(\widehat{B}\)bù nhau \(\Rightarrow\widehat{A}+\widehat{B}=180^0\)
Theo bài ra ta có:
\(4\widehat{A}=5\widehat{B}\Rightarrow\frac{\widehat{A}}{5}=\frac{\widehat{B}}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau và \(\widehat{A}+\widehat{B}=180^0\), ta có:
\(\frac{\widehat{A}}{5}=\frac{\widehat{B}}{4}=\frac{\widehat{A}+\widehat{B}}{5+4}=\frac{180^0}{9}=20^0\)
Từ \(\frac{\widehat{A}}{5}=20^0\Rightarrow\widehat{A}=20^0.5=100^0\)
\(\frac{\widehat{B}}{4}=20^0\Rightarrow\widehat{B}=20^0.4=80^0\)
Vậy \(\widehat{A}=100^0;\widehat{B}=80^0\)
4A = 5B = 180
A = 180 : ( 5 + 4 ) x 5 = 100
B = 180 - 100 = 80
Đúng 100%
Đúng 100%
Đúng 100%

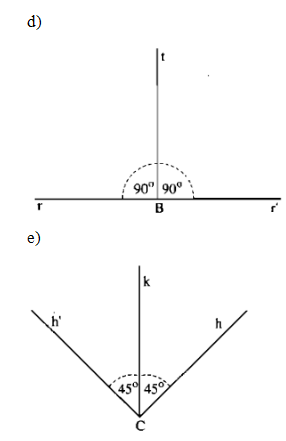
Bài tập dạng này có nhiều trường hợp về hình vẽ. Chỉ yêu cầu HS vẽ đúng một trường hợp, riêng với các ý c, d, và e chú ý có 2 trường hợp về hình vẽ:

a.Ta co : 3/5=3.3/5.3=9/15
=>3/5=9/15
b. Ta co : Goc: A + C =60o+30o=90o
Vay goc A va goc C la hai goc phu nhau.

a) \(\widehat{A}\)và \(\widehat{B}\)bù nhau
\(\Rightarrow\widehat{A}+\widehat{B}=180^o\)
mà \(\widehat{A}-\widehat{B}=30^o\)
\(\Rightarrow\widehat{A}=\frac{180^o+30^o}{2}=105^0\)
\(\Rightarrow\widehat{B}=180^o-105^o=75^o\)
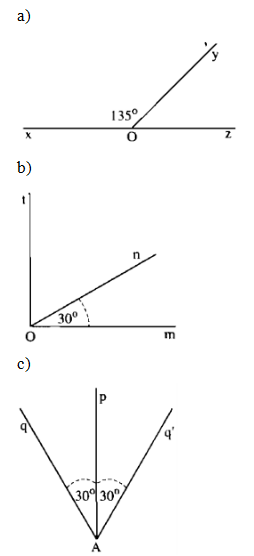
Vì \(\widehat A\) và \(\widehat B\) bù nhau nên \(\widehat A+\widehat B=180^\circ\) (1)
Lại có: \(\widehat A-\widehat B=30^\circ\) (2)
Từ (1) và (2) \(\Rightarrow (\widehat A+\widehat B)+(\widehat A-\widehat B)=180^\circ+30^\circ\)
\(\Rightarrow2\widehat{A}=210^{\circ}\)
\(\Rightarrow\widehat{A}=\dfrac{210^{\circ}}{2}=105^{\circ}\)
Khi đó: \(105^{\circ}-\widehat{B}=30^{\circ}\Rightarrow\widehat{B}=105^{\circ}-30^{\circ}=75^{\circ}\)
Tính số đo các góc A và B biết rằng chúng bù nhau