Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số cạnh của đa giác là n ta có
Số đo của n góc trong là
180.(n - 2)
Số đo 1 góc trong là (đa giác đều)
\(\frac{180\left(n-2\right)}{n}\)
Số do 1 góc ngoài là
\(180-\frac{180\left(n-2\right)}{n}=\frac{360}{n}\)
Theo đề bài ta có
\(\frac{360n}{n}+\frac{180\left(n-2\right)}{n}=500\)
\(\Leftrightarrow n=9\)
Tổng số đo các góc ngoài của đa giác bằng 360 0
Số đo một góc trong của đa giác đều là 468 0 – 360 0 = 108 0
Gọi n là số cạnh của đa giác đều. Ta có số đo mỗi góc của đa giác đều bằng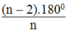 
Suy ra: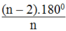
=
108
0
⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5
Vậy đa giác đều cần tìm có 5 cạnh.
Cho đa giác có tổng số đo các góc trong bằng 5 lần tổng các góc ngoài .Hỏi đa giác có bao nhiêu cạnh
Gọi số cạnh của đa giác là \(n\left(n\ge3,n\in N\right)\)
Tổng các góc ngoài của 1 đa giác luôn là 360 độ
Tổng số đo các góc trong của đa giác n cạnh là \(\left(n-2\right).180^0\)
Theo bài ra, ta có: \(\left(n-2\right).180^0=360^0.5\)
\(\Rightarrow\left(n-2\right).180^0=1800^0\Rightarrow n-2=10\Rightarrow n=12\) (thỏa mãn)
Vậy đa giác đó có 12 cạnh
Gọi số cạnh của đa giác đó là n
Ta có
n(n-3)/2=2n
=> n=7
KL
có thể giải kĩ câu trả lời ra được không