
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tính nhanh (2/3+3/4+5/6+...+99/100).(1/2+2/3+3/4+...+98/99)-(1/2+1/3+...+99/100).(2/3+2/4+...+98/99)



Đặt A = 1.2 + 2.3 + 3.4 +.......... + 99.100
=> 3A = 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + ..... + 99.100.(101 - 98)
=> 3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ....... + 99.100.101 - 98.99.100
=> 3A = (1.2.3 + 2.3.4 + 3.4.5 + ....... + 99.100.101) - (1.2.3 + 2.3.4 + ......... + 98.99.100)
=> 3A = 99.100.101
=> A = 99.100.101 : 3 = 999900
2/11x13+2/13x15+2/15x17+....+2/95x97+2/97x99
=1/11-1/13+1/13-1/15+1/15-1/17+....+1/95-1/97+1/97-1/99
=1/11-1/99
=9/99-1/99
=8/99
đúng nhé bạn

1 + 2 + 3 + 4 + ... + 999 + 1000 - 1 - 2 - 3 - 4 - ... - 99 - 100
= (1 - 1) + (2 - 2) + (3 - 3) + (4 - 4) + ... + (99 - 99) + (100 - 100) + 101 + 102 + 103 + ... + 999 + 1000
= 101 + 102 + 103 + ... + 999 + 1000
= \(\frac{\left(101+1000\right)\times900}{2}=495450\)

a
so so hang
(100-1):1+1=100(so hang)
tong bang
(100+1)x100:2=5050

\(D=\frac{1}{2}+\frac{1}{2.3}+\frac{1}{3.4}+...\frac{1}{99.100}\)
\(D=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}...\frac{1}{99}-\frac{1}{100}\)
\(D=\frac{1}{1}-\frac{1}{100}\)
\(D=\frac{99}{100}\)
Vậy tổng D bằng \(\frac{99}{100}\)
tổng quát: \(\frac{1}{n\left(n+1\right)}=\frac{1}{n}-\frac{1}{n+1}\)
áp dụng ta có: \(D=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}\)
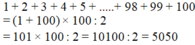
\(\frac{2}{1.2}+\frac{2}{2.3}+\frac{2}{3.4}+...+\frac{2}{99.100}\)
\(=2\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\right)\)
\(=2\left(1-\frac{1}{100}\right)\)
\(=2.\frac{99}{100}\)
\(=\frac{99}{50}\)
Đầu tiên đặt 2 ra
Đặt bt còn lại là ...
Tách 1/ 1×2=1-1/2; 1/2×3=1/2-1/3....1/99×100=1/99-1/100
=1/1-1/100
=...