Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = 1/2 + 1/4 + 1/8 + ... + 1/1024
2A = 1 + 1/2 + 1/4 + ... + 1/512
2A - A = (1 + 1/2 + 1/4 + ... + 1/512) - (1/2 + 1/4 + 1/8 + ... + 1/1024)
A = 1 - 1/1024
A = 1023/1024
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+....+\frac{1}{1024}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+......+\frac{1}{512}\)
\(\Rightarrow A=2A-A=1-\frac{1}{1024}\)
\(A=\frac{1023}{1024}\)

\(\frac{3}{2}+\frac{3}{4}+\frac{3}{8}+\frac{3}{16}+\frac{3}{32}+\frac{3}{64}+\frac{3}{128}+\frac{3}{256}+\frac{3}{512}+\frac{3}{1024}\)
=\(3.\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256}+\frac{1}{512}+\frac{1}{1024}\right)\)
=\(3.\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\frac{1}{16}-\frac{1}{32}+\frac{1}{32}-\frac{1}{64}+\frac{1}{64}-\frac{1}{128}+\frac{1}{128}-\frac{1}{256}+\frac{1}{256}-\frac{1}{512}+\frac{1}{512}-\frac{1}{1024}\right)\)
=\(3.\left(1-\frac{1}{1024}\right)=3.\left(\frac{1024}{1024}-\frac{1}{1024}\right)=3.\frac{1023}{1024}=\frac{3069}{1024}\)
Chúc em học tốt

gọi A=1/2+1/4+1/8+...+1/1024
2xA=1+1/2+1/4+.....+1/512
2xA-A=(1+1/2+1/4+....+1/512)-(1/2+1/4+1/8+...+1/1024)
A=1-1/1024
=1023/1024
vậy A=1023/1024
\(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{1024}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+...+\frac{1}{512}-\frac{1}{1024}=1-\frac{1}{1024}=\frac{1023}{1024}\)

đặt biểu thức là A ta có :
A = 1/2 + 1/4 + 1/8 + 1/16 +1/32 +1/64 +1/128 + 1/256 + 1/512 + 1/102
A x 2 = 1+ 1/2 + 1/4 + 1/8 + 1/16 +1 /32+1/64 + 1/ 128 + 1/256 + 1/512
A = ( 1 + 1/2 +1/4 + 1/ 8+ 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 ) - ( 1/2 + 1/4 + 1/8 +1/16 +1/32 + 1/64 + 1/128 +1/256 +1/512 +1/1024)
A = 1 - 1/1024
A = 1023/1024
nhớ k nhé
(1 / 2) + (1 / 4) + (1 / 8) + (1 / 16) + (1 / 32) + (1 / 64) + (1 / 128) + (1 / 256) + (1 / 512) + (1 / 1024) =
0.9990234375

đề phải là 1 +1/2 + 1/4 +1/32 + 1/64 + 1/128 +1/256 +/512 +1/1024 moi dug
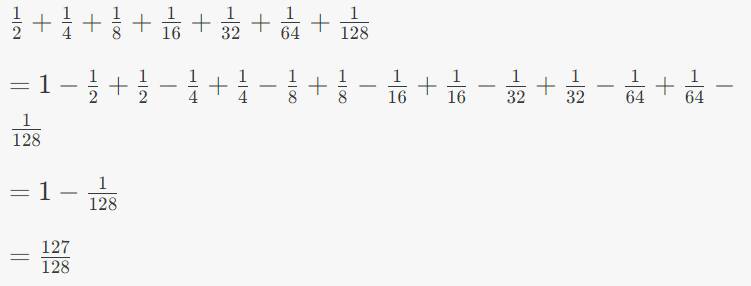
Đặt
\(S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{1024}\)
ta có : \(2S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+..+\frac{1}{512}=1-\frac{1}{1024}+\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{1024}\right)\)
\(=1-\frac{1}{1024}+S\text{ nên }S=1-\frac{1}{1024}=\frac{1023}{1024}\)