K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
30 tháng 9 2021
\(20,1\cdot19,9=\left(20-0,1\right)\left(20+0,1\right)=20^2-0,1^2=400-0,01=399,01\\ 31,8^2-2\cdot31,8\cdot21,8+21,8^2=\left(31,8-21,8\right)^2=10^2=100\\ 33,3^2-2\cdot33,3\cdot3,3+3,3^2=\left(33,3-3,3\right)^2=30^2=900\)
LT
1
6 tháng 11 2017
Đổi: \(40'=\frac{2}{3}h\)
Vận tốc là:
\(3,6:\frac{2}{3}=5,4\)km/giờ
Đáp số: 5,4 km/giờ
P/s: Ko chắc nx
17 tháng 10 2016
A= 2006 X 2008 - 20072
A = 2006 . 2008 - 2007 . 2007
A = 2006 . ( 2007 + 1 ) - 2007 . ( 2006 + 1 )
A = 2006 . 2007 + 2006 - 2007 . 2006 + 2007
A = -1
B= 2016 X 2018 - 20172
B= 2016 . 2018 - 2017 . 2017
B = 2016 . ( 2017 + 1 ) - 2017 . ( 2016 + 1 )
B = 2016 . 2017 + 2016 - 2017 . 2016 + 2017
B = -1
26 tháng 10 2021
a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành
PN
14 tháng 2 2016
\(a.\) Từ \(x-2y=1\) \(\Rightarrow\) \(x=1+2y\) \(\left(\text{*}\right)\)
Thay \(x=1+2y\) vào \(A\), khi đó, biểu thức \(A\) trở thành
\(A=\left(1+2y\right)^2+y^2+4=1+4y+4y^2+y^2+4=5y^2+4y+5\)
\(A=5\left(y^2+\frac{4}{5}y+1\right)=5\left(y^2+2.\frac{2}{5}.y+\frac{4}{25}+\frac{21}{25}\right)=5\left(y+\frac{2}{5}\right)^2+\frac{21}{5}\ge\frac{21}{5}\) với mọi \(y\)
Dấu \(''=''\) xảy ra \(\Leftrightarrow\) \(\left(y+\frac{2}{5}\right)^2=0\) \(\Leftrightarrow\) \(y+\frac{2}{5}=0\) \(\Leftrightarrow\) \(y=-\frac{2}{5}\)
Thay \(y=-\frac{2}{5}\) vào \(\left(\text{*}\right)\), ta được \(x=\frac{1}{5}\)
Vậy, \(A\) đạt giá trị nhỏ nhất là \(A_{min}=\frac{21}{5}\) khi và chỉ khi \(x=\frac{1}{5}\) và \(y=-\frac{2}{5}\)
\(b.\) Gọi \(Q\left(x\right)\) là thương của phép chia và dư là \(r=ax+b\) (vì dư trong phép chia cho \(x^2-1\) có bậc cao nhất là bậc nhất), với mọi \(x\) ta có:
\(x^{2008}-x^3+5=\left(x^2-1\right).Q\left(x\right)+ax+b\) \(\left(\text{**}\right)\)
Với \(x=1\) thì phương trình \(\left(\text{**}\right)\) trở thành \(5=a+b\) \(\left(1\right)\)
Với \(x=-1\) thì phương trình \(\left(\text{**}\right)\) trở thành \(7=-a+b\) \(\left(2\right)\)
Giải hệ phương trình \(\left(1\right)\) và \(\left(2\right)\), ta được \(a=-1\) và \(b=6\)
Vậy, dư trong phép chia đa thức \(x^{2008}-x^3+5\) cho đa thức \(x^2-1\) là \(-x+6\)
D
19 tháng 1 2022
a) Ta có: BE+CE=BC
=>BC=20+15=35 (cm)
Ta có: DE vuông góc với AB (gt)
AC vuông góc với AB (tam giác ABC vuông tại A)
=>DE//AC
Xét tam giác ABC có:
DE//AC (cmt)
=>\(\dfrac{BD}{AB}=\dfrac{BE}{BC}\)(định lý Ta-let)
=>\(\dfrac{16}{AB}=\dfrac{20}{35}\)
=>AB=28 (cm)
b. Xét tứ giác ADEK có:
góc ADE=góc DAK=góc AKE=900
=>ADEK là hình chữ nhật.
c. Ta có: AB=BD+AD
=>28=16+AD
=>AD=12(cm)
Xét tam giác ABC vuông tại A có:
AB2+AC2=BC2(định lý Ta-let)
=>282+AC2=352
=>AC=21 (cm)
Xét tam giác ABC có:
DE//AC (cmt)
=>\(\dfrac{BD}{AB}=\dfrac{DE}{AC}\)(định lý Ta-let)
=>\(\dfrac{16}{28}=\dfrac{DE}{21}\)
=>DE=12(cm)
*SADEK=AD.DE=12.12=144(cm)
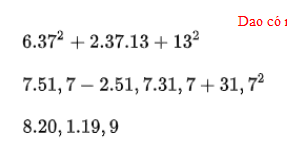
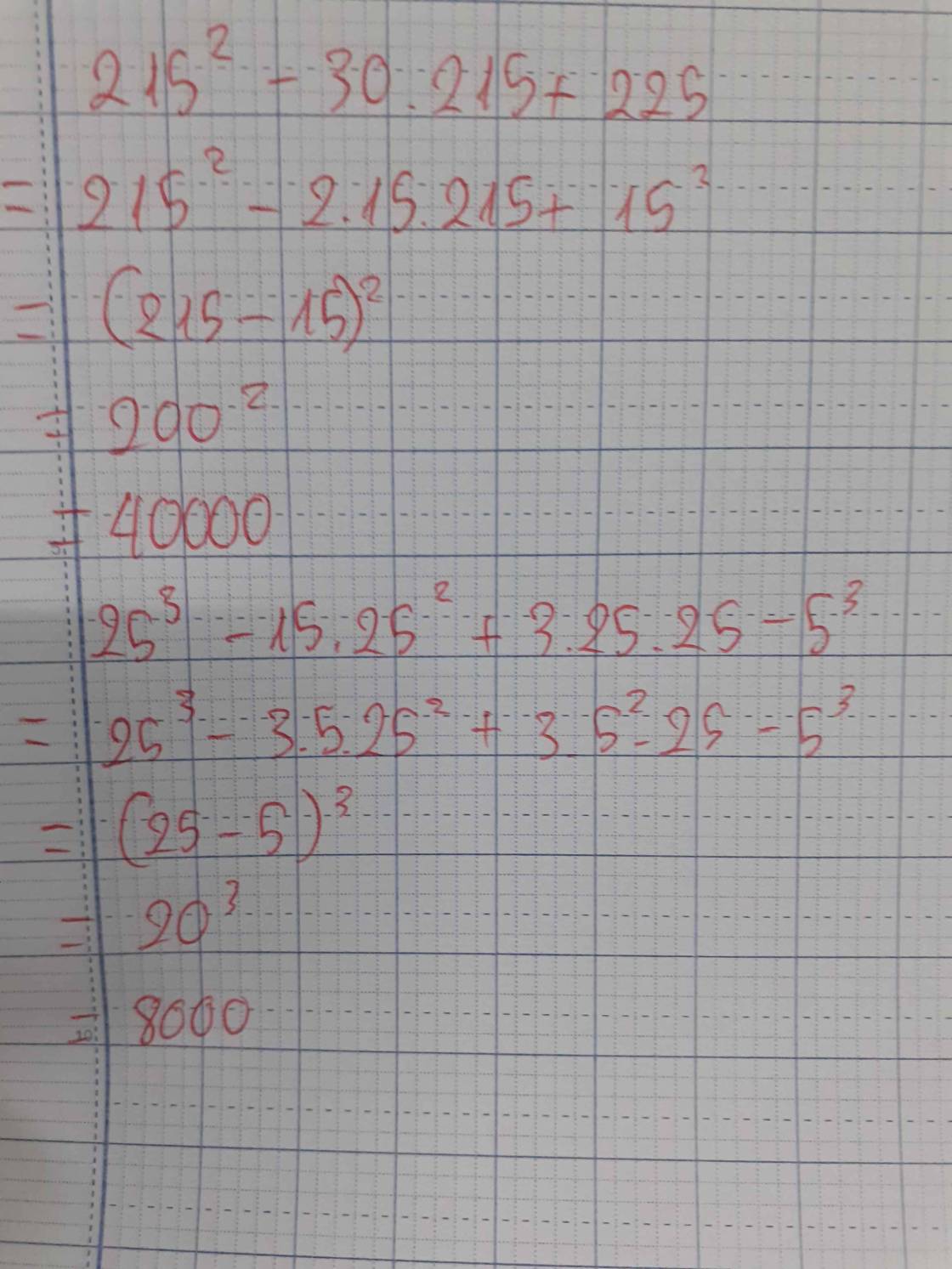
\(37^2+2\cdot37\cdot13+13^2=\left(37+13\right)^2=50^2=2500\\ 51,7-2\cdot51,7\cdot31,7+31,7=\left(51,7-31,7\right)^2=20^2=400\\ 20,1\cdot19,9=\left(20+0,1\right)\left(20-0,1\right)=20^2-0,1^2\\ =400-0,01=399,01\)