H
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 6 2022
a: \(=-3x^3y^3-3x^2y^2+2x^2y\)
b: \(=6x^2+12x-2x-4\)
\(=6x^2+10x-4\)
c: \(=6x^3y^3+10x^2y^2-2x^2y\)
d: \(=2x^2-3x-2x+3\)
\(=2x^2-5x+3\)
Q
21 tháng 4 2017
a) \((2x^2−3x)(5x^2−2x+1)\)
\(=2x^2.5x^2−2x^2.2x+2x^2−3x.5x^2+3x.2x−3x\)
\(=10x^4−4x^3+2x^2−15x^3+6x^2−3x\)
\(=10x^4−19x^3+8x^2−3x\)
b) \((x−2y)(3xy+5y^2+x)\)
\(=x.3xy+x.5y^2+x.x−2y.3xy−2y.5y^2−2y.x\)
\(=3x^2y+5xy^2+x^2−6xy^2−10y^3−2xy\)
\(=3x^2y−xy^2−2xy+x^2−10y^3\)
HQ
Hà Quang Minh
Giáo viên
12 tháng 1
a)
\(\begin{array}{l}\left( {2x - 5y} \right)\left( {2x + 5y} \right) + {\left( {2x + 5y} \right)^2}\\ = \left( {2x + 5y} \right)\left( {2x - 5y + 2x + 5y} \right)\\ = \left( {2x + 5y} \right).4x\\ = 2x.4x + 5y.4x\\ = 8{x^2} + 20xy\end{array}\)
b)
\(\begin{array}{l}\left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right) + \left( {2x - y} \right)\left( {4{x^2} + 2xy + {y^2}} \right)\\ = {x^3} + {\left( {2y} \right)^3} + {\left( {2x} \right)^3} - {y^3}\\ = {x^3} + 8{y^3} + 8{x^3} - {y^3}\\ = \left( {{x^3} + 8{x^3}} \right) + \left( {8{y^3} - {y^3}} \right)\\ = 9{x^3} + 7{y^3}\end{array}\)
8 tháng 9 2023
Bạn xem lại đề nhé.
a) \(A=x^2+5y^2+2xy-4x-8y+2015\)
\(A=x^2-4x+4-2y\left(x-2\right)+y^2+2011+4y^2\)
\(A=\left(x-2\right)^2-2y\left(x-2\right)+y^2+2011+4y^2\)
\(A=\left(x-2-y\right)^2+4y^2+2011\)
Vì \(\left(x-y-2\right)^2\ge0;4y^2\ge0\)
\(\Rightarrow A_{min}=2011\)
Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}x-y-2=0\\4y^2=0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
22 tháng 7 2023
`a, = 3x^2y - 3xy + 6x^2y + 5xy - 9x^2y`
`= 2xy`.
Thay `x = 2/3; y = -3/4` vào BT:
`2 . 2/3 . -3/4 = -1.`
`b, x(x-2y) - y(y^2-2x)`
`= x^2 - 2xy - y^3 + 2xy`
`= x^2 - y^3`
Thay `x = 5; y =3` vào BT:
`= 5^2 - 3^3 = 25 - 27 = -2`
H9
HT.Phong (9A5)
CTVHS
22 tháng 7 2023
a) \(3x^2y-\left(3xy-6x^2y\right)+\left(5xy-9x^2y\right)\)
\(=3x^2y-3xy+6x^2y+5xy-9x^2y\)
\(=2xy\)
Thay \(x=\dfrac{2}{3},y=-\dfrac{3}{4}\) vào Bt ta có:
\(2\cdot\dfrac{2}{3}\cdot-\dfrac{3}{4}=-1\)
b) \(x\left(x-2y\right)-y\left(y^2-2x\right)\)
\(=x^2-2xy-y^3+2xy\)
\(=x^2-y^3\)
Thay \(x=5,y=3\) vào Bt ta có:
\(5^2-3^3=-3\)
14 tháng 8 2021
a: \(3x^2y\left(2x^2-xy+5y^2\right)=6x^4y-3x^3y^2+15x^2y^3\)
b: \(\left(x+2\right)\left(x^2+3x-4\right)\)
\(=x^3+3x^2-4x+2x^2+6x-8\)
\(=x^3+5x^2+2x-8\)
4 tháng 9 2022
a: \(=2x^2-x+5\)
b: \(=-\dfrac{3}{2}x^3+x^2-\dfrac{1}{2}x\)
c: \(=-x^3+\dfrac{3}{2}-2x\)
d: \(=-2x^2+4xy-6y^2\)
e: \(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)
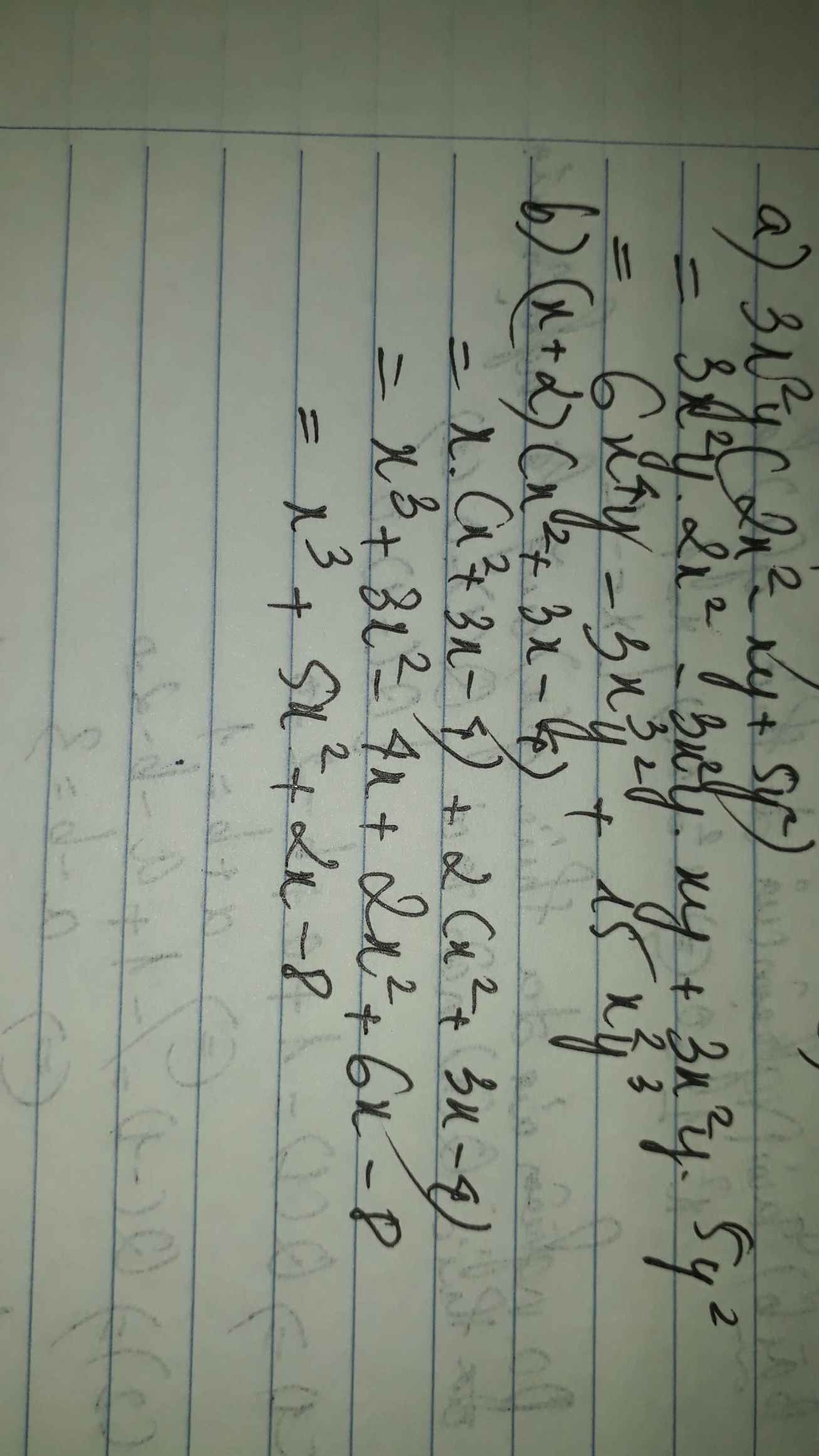
\(\left(x^3+2x^5y^2-4\right)\left(-3xy\right)\)
\(=-3x^{3+1}y-3.2x^{5+1}y^{2+1}+\left(-4\right).-3xy\)
\(=3x^4y-6x^6y^3+12xy\)