
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


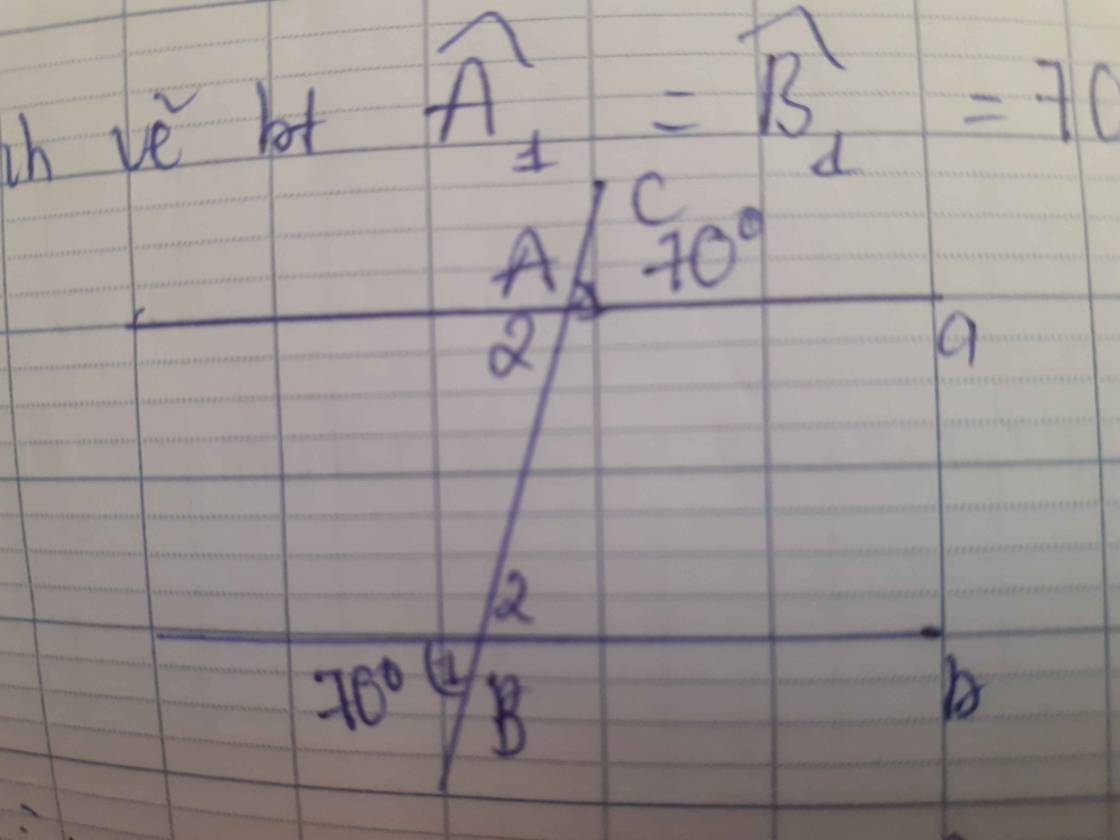
Ta có:
∠B₂ = ∠B₁ = 70⁰ (đối đỉnh)
⇒ ∠B₂ = ∠A₁ = 70⁰
Mà ∠B₂ và ∠A₁ là hai góc đồng vị
⇒ a // b

a) Dấu hiệu: Thời gian làm một bài tập của mỗi học sinh
b) Bảng tần số:
| Giá trị(x) | Tần số(n) |
| 5 | 2 |
| 7 | 4 |
| 8 | 5 |
| 9 | 4 |
| 10 | 3 |
| 12 | 2 |
N=20
c) Số trung bình cộng: \(\dfrac{5.2+7.4+8.5+9.4+10.3+12.2}{20}=8,4\)
Mốt của dấu hiệu là 8.
a) Dấu hiệu: Thời gian làm một bài tập của mỗi học sinh
b) Bảng tần số:
| Giá trị(x) | Tần số(n) |
| 5 | 2 |
| 7 | 4 |
| 8 | 5 |
| 9 | 4 |
| 10 | 3 |
| 12 | 2 |
N=20
c) Số trung bình cộng: 5.2+7.4+8.5+9.4+10.3+12.220=8,45.2+7.4+8.5+9.4+10.3+12.220=8,4
Mốt của dấu hiệu là 8.

a,
Cách 1: Vì △ABC đều => AB = AC = BC = 5 cm
Theo tính chất △ đều thì đường cao trong △ đều chính là đường trung tuyến => HA = HC = AC : 2 = 5 : 2 = 2,5 (cm)
Xét △BHA vuông tại H có: AH2 + BH2 = AB2 (định lý Pytago)
=> (2,5)2 + BH2 = 52 => 6,25 + BH2 = 25 => BH2 = 18,75 => BH = \(\frac{5\sqrt{3}}{2}\approx4,3\)(cm)
Cách 2: Áp dụng công thức \(h=a\frac{\sqrt{3}}{2}\) (h là đg` cao; a là chiều dài cạnh △ đều)
\(\Rightarrow BH=\frac{5\sqrt{3}}{2}\approx4,3\)(cm)
b,
Vì △ABC đều => ABC = ACB = BAC = 60o
Theo tính chất △ đều thì đường cao trong △ đều chính là chính là đường phân giác của góc ở đỉnh.
=> BH là phân giác ABC => ABH = HBC = ABC : 2 = 60o : 2 = 30o
Ta có: ABK + ABH = 180o (2 góc kề bù) => ABK + 30o = 180o => ABK = 150o
Và KBC + CBH = 180o (2 góc kề bù) => KBC + 30o = 180o => KBC = 150o
Lại có: AB = BK = BC = 5 cm
=> △ABK cân tại B (1) và △KBC cân tại B (2)
(1) => BKA = (180o - KBA) : 2 = (180o - 150o) : 2 = 30o : 2 = 15o
(2) => BKC = (180o - KBC) : 2 = (180o - 150o) : 2 = 30o : 2 = 15o
Ta có: AKC = BKA + BKC = 15o + 15o = 30o
Lại có: ABC + AKC = 60o + 30o = 90o


Vì a; b; c à các góc của tam giác => a + b + c = 1800
Ta có : a=b=2c⇒a2=b2=c1a=b=2c⇒a2=b2=c1
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
a2=b2=c1=a+b+c2+2+1=18005=360a2=b2=c1=a+b+c2+2+1=18005=360
⇒{a=b=72c=36⇒{a=b=72c=36
Vậy....
Bạn @๖ACE✪ミ★乙ᑌᑎᗴ⁀ᶦᵈᵒᶫ❄丅ᖇưởᑎǤ❄丅ᗴᗩᗰ❄(❄丅ᗴᗩᗰ❄ᑕᑌ丅ᗴ❄)ঔৣ✞ có thể giúp mình viết kĩ và đầy đủ hơn đc ko bn. Mình ko hiểu khá nhiều chỗ còn dãy tỉ số = nhau thì ok r. Bn giải lại r mk tích cho.
Tính các góc nhọn tam giác ABC vuông tại A có đg cao AH biết HC-HB=AB
Giúp mình với mình đang cần gấp

Tham Khảo:
Lời giải:
Tập xác định của phương trình
Biến đổi vế trái của phương trình
Phương trình thu được sau khi biến đổi
Rút gọn thừa số chung
Đơn giản biểu thức
Giải phương trình
Lời giải thu được

Vì \(\Delta ABC\)cân tại \(A\left(gt\right)\)
\(\Rightarrow\widehat{B}=\widehat{C}\)
Xét \(\Delta ABC\)có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{B}-30+\widehat{B}+\widehat{B}=180^0\)
\(\Rightarrow3\widehat{B}-30=180^0\)
\(\Rightarrow3\widehat{B}=210^0\)
\(\Rightarrow\widehat{B}=70^0\)
học tốt
 bn nào làm hộ mình với mình đang cần gấp.
bn nào làm hộ mình với mình đang cần gấp.
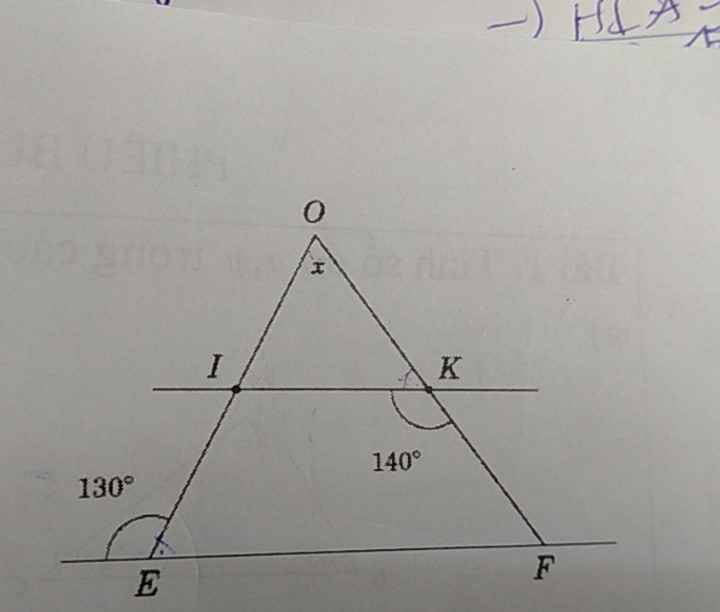
IK//EF
=>\(\widehat{IKF}+\widehat{OFE}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{OFE}+140^0=180^0\)
=>\(\widehat{OFE}=40^0\)
\(\widehat{IEF}+\widehat{E_1}=180^0\)(hai góc kề bù)
=>\(\widehat{IEF}+130^0=180^0\)
=>\(\widehat{IEF}=50^0\)
Xét ΔOEF có \(\widehat{EOF}+\widehat{FEO}+\widehat{EFO}=180^0\)
=>\(x+50^0+40^0=180^0\)
=>\(x=90^0\)
Lời giải:
Bổ sung điều kiện: $IK\parallel EF$.
Vì $IK\parallel EF$ nên:
$\widehat{OIK}=\widehat{OEF}$ (2 góc đồng vị)
$=180^0-130^0=50^0$
$\widehat{OKI}=180^0-\widehat{IKF}=180^0-140^0=40^0$
Xét tam giác $OIK$ thì:
$x=180^0-(\widehat{OIK}+\widehat{OKI})=180^0-(50^0+40^0)=90^0$