Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=1-8x-x^2=-\left(x^2+8x+16\right)+17=-\left(x-4\right)^2+17\le17\)
\(ĐTXR\Leftrightarrow x=4\)
b) \(B=5-2x+x^2=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
\(ĐTXR\Leftrightarrow x=1\)
c) \(C=x^2+4y^2-6x+8y-2021=\left(x^2-6y+9\right)+\left(4y^2+8y+4\right)-2034=\left(x-3\right)^2+\left(2y+2\right)^2-2034\ge-2034\)
\(ĐTXR\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
a: Ta có: \(A=-x^2-8x+1\)
\(=-\left(x^2+8x-1\right)\)
\(=-\left(x^2+8x+16-17\right)\)
\(=-\left(x+4\right)^2+17\le17\forall x\)
Dấu '=' xảy ra khi x=-4
b: Ta có: \(x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1


c: \(-x^2+2x-2=-\left(x-1\right)^2-1\le-1\forall x\)
\(\Leftrightarrow V\ge-1\forall x\)
Dấu '=' xảy ra khi x=1


My Nguyễn ơi,bạn truy cập vào đường link này để tìm câu hỏi tương tự của câu a/Bài 1 nhé
https://vn.answers.yahoo.com/question/index?qid=20110206184834AAokV5m&sort=N

a )\(A=2x^2-8x-10=2\left(x^2-4x-5\right)=2\left[\left(x^2-4x+4\right)-9\right]\)
\(=2\left[\left(x-2\right)^2-9\right]=2\left(x-2\right)^2-18\)
Vì \(2\left(x-2\right)^2\ge0\forall x\) nên \(A=2\left(x-2\right)^2-18\ge-18\forall x\)
Dấu "=" xảy ra <=> \(2\left(x-2\right)^2=0\Leftrightarrow x=2\)
Vậy GTNN của A là - 18 tại x = 2
b ) \(B=9x-3x^2=-3\left(x^2-3x\right)=-3\left[\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{4}\right]\)
\(=-3\left[\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{4}\right]=-3\left(x-\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
Vì \(\cdot3\left(x-\dfrac{3}{2}\right)^2\le0\forall x\) nên \(B=-3\left(x-\dfrac{3}{2}\right)^2+\dfrac{27}{4}\le\dfrac{27}{4}\)
Dấu "=" xảy ra <=> \(-3\left(x-\dfrac{3}{2}\right)^2=0\Rightarrow x=\dfrac{3}{2}\)
Vậy GTLN của B là \(\dfrac{27}{4}\) tại x = \(\dfrac{3}{2}\)

\(A=2\left(x^2-4x+4\right)-7=2\left(x-2\right)^2-7\ge-7\)
Dấu \("="\Leftrightarrow x=2\)
\(B=\left(x^2+3x+\dfrac{9}{4}\right)-\dfrac{1}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=-\dfrac{3}{2}\)
\(C=4\left(x^2-2x+1\right)-4=4\left(x-1\right)^2-4\ge-4\)
Dấu \("="\Leftrightarrow x=1\)
\(D=\dfrac{1}{-\left(x^2+2x+1\right)+6}=\dfrac{1}{-\left(x+1\right)^2+6}\ge\dfrac{1}{6}\)
Dấu \("="\Leftrightarrow x=-1\)
1.
$A=2x^2-8x+1=2(x^2-4x+4)-7=2(x-2)^2-7$
Vì $(x-2)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A\geq 2.0-7=-7$
Vậy $A_{\min}=-7$ khi $x-2=0\Leftrightarrow x=2$
2.
$B=x^2+3x+2=(x^2+3x+1,5^2)-0,25=(x+1,5)^2-0,25\geq 0-0,25=-0,25$
Vậy $B_{\min}=-0,25$ khi $x=-1,5$
3.
$C=4x^2-8x=(4x^2-8x+4)-4=(2x-2)^2-4\geq 0-4=-4$
Vậy $C_{\min}=-4$ khi $2x-2=0\Leftrightarrow x=1$
4. Để $D_{\min}$ thì $5-x^2-2x$ là số thực âm lớn nhất
Mà không tồn tại số thực âm lớn nhất nên không tồn tại $x$ để $D_{\min}$
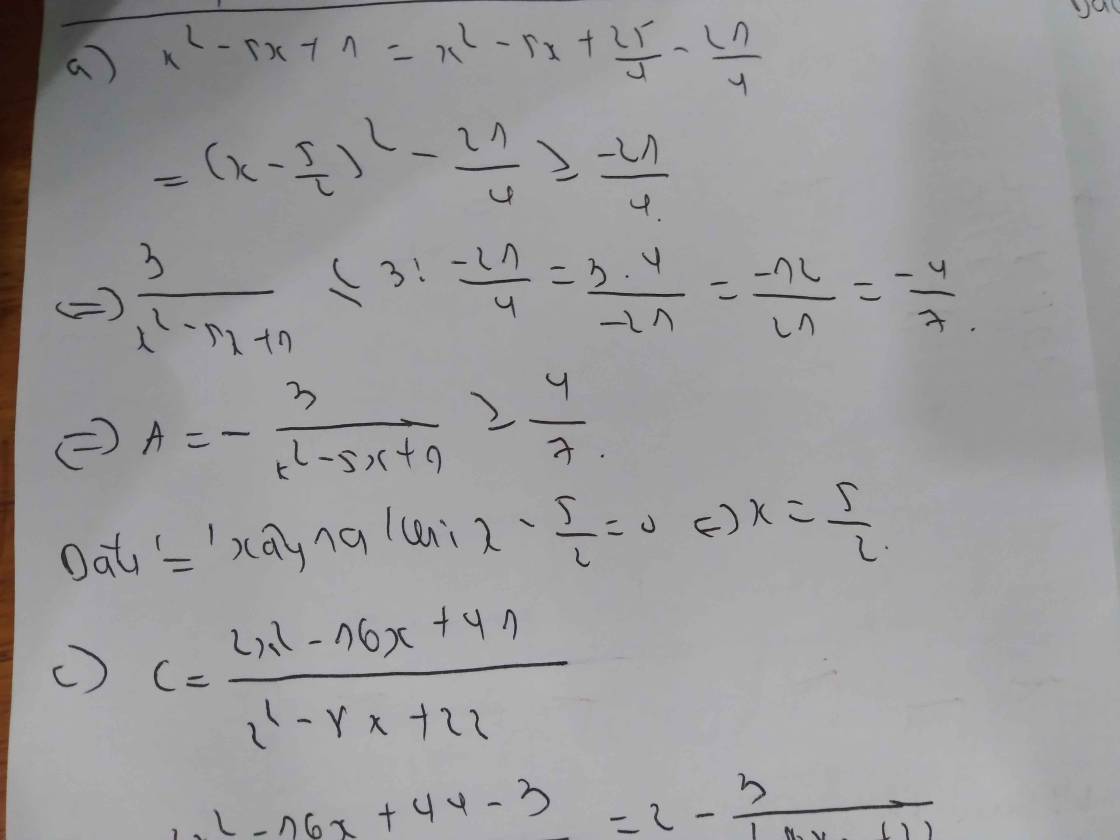
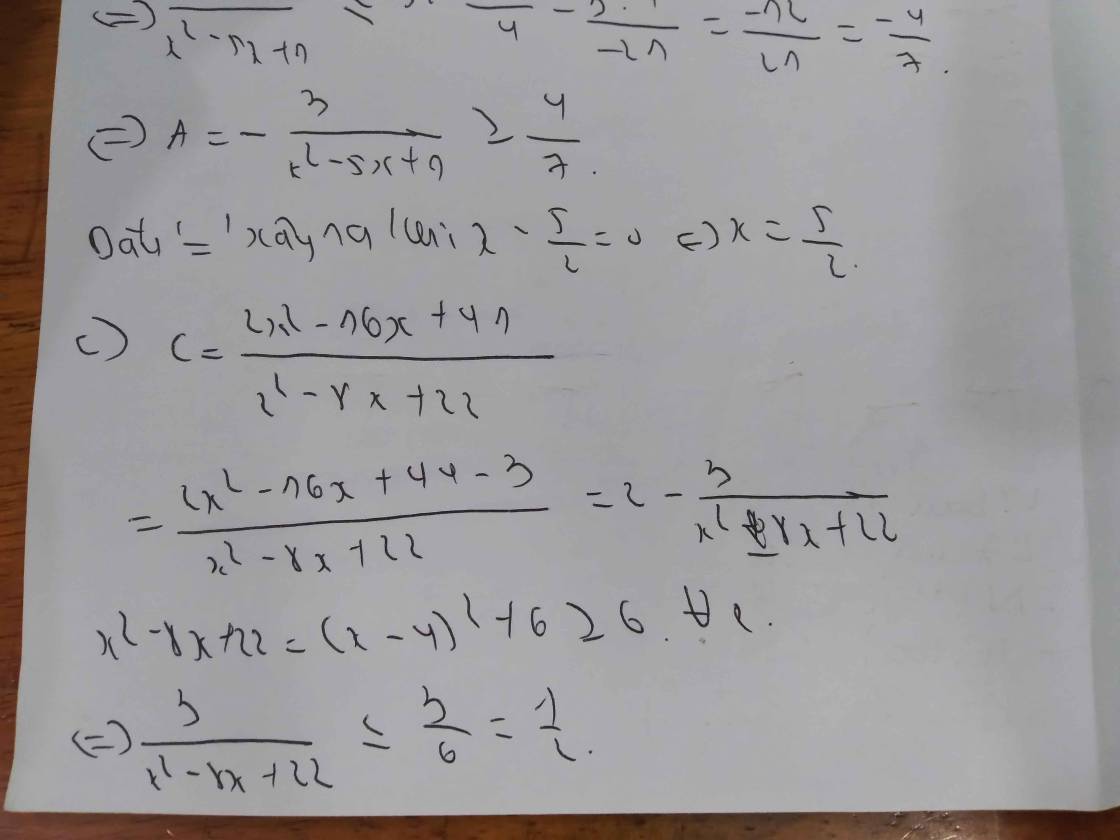
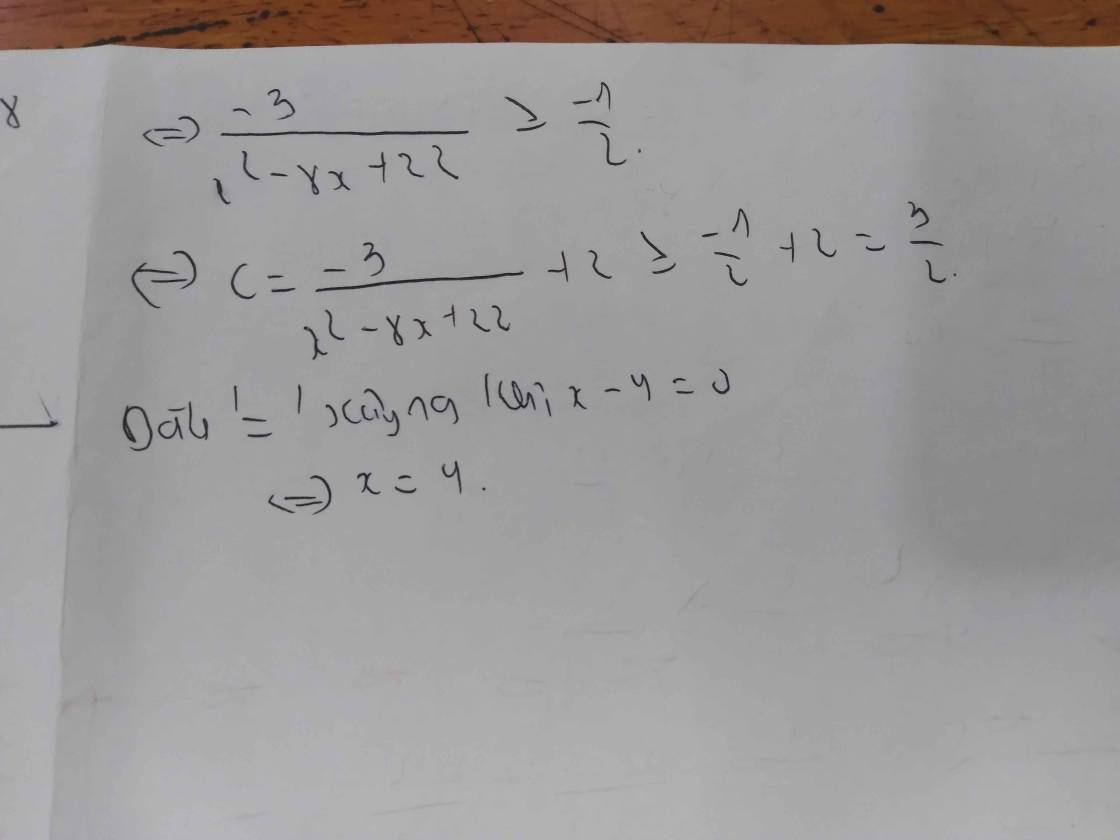
b) B=-3(x^2-3x+9/4)+27/4=-3(x-3/2)^2+27/4 <=27/4. Vậy MaxB=27/4, dấu "=" xảy ra <=> x-3/2=0 <=> x=3/2
a, Ta có : \(A=2x^2-8x-10=2\left(x^2-4x-5\right)\)
\(=2\left(x^2-4x+4-9\right)=3\left(x-2\right)^2-18\ge-18\)
Dấu ''='' xảy ra <=> x = 2
Vậy GTNN A là -18 <=> x = 2