PB
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
11 tháng 6 2018
Thay x = -1 vào biểu thức đã cho ta được:
(-1) + ( -1)3 + (-1)5 + (-1)7 +...+ (-1)101
= (-1) + (-1) + (-1) + (-1) +(- 1)+ ... + (-1) (51 số -1)
= -51.
Chọn đáp án C
TC
7 tháng 5 2022
Câu 12. Giá trị của đa thức
x + x3 + x5 + x7 + ... + x101 tại x = -1 là
A. -101. B.
-100 . C.
-51 . D.
-50 .
Câu 13. Trong các biểu thức sau, biểu thức nào không là đơn thức?
A. y4 z6 . B.
-2y4z . C. (yz)10 . D.
-2(y + z) .
Câu 14. Đa thức 6y3 + 6x + 4 - 8x + 5 + 9y3 được thu gọn thành
A. 15y3 + 14x + 9 . B. -3y6 - 2x2 + 9 . C. 15y3 - 2x + 9 . D. 15y3 - 2x -1 .
Câu 15. Đơn thức
- 7 y3x có hệ số và phần biến là:
2
A. - 7
2
và y3x . B. 7 2
và -y3x . C. - 7 2
và -y3x . D. 7 2
và y3x .
Câu 16. Thu gọn và tìm bậc của đa thức -y2 + 4y + 8 - 6y - 6y2 -1:
A. -7y2 +10y + 7 , bậc 3 . B. -7y2 - 2y + 7 , bậc 2 .
C. 5y4 - 2y2 + 7 , bậc 4 . D. -7y2 - 2y - 9 , bậc 2 .
Câu 17. Đa thức (9x3 - 5x - 5) - (4x2 - 5x + 4)
thu gọn là
A. 9x3 - 4x2 -10x - 9 . B. 9x3 - 4x2 - 9 .
C. 9x3 + 4x2 - 9 .
HK
2
PT
1 tháng 7 2021
Thay x = 1 vào f(x) ta được
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
1 tháng 7 2021
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
CM
18 tháng 10 2017
Thay x = 1 vào f(x) ta được
f ( 1 ) = 1 + 1 3 + 1 5 + 1 7 + … + 1 101 = 1 + 1 + 1 + … + 1 ⏟ 51501 = 51.1 = 51
Thay x = -1 vào f(x) ta được
f ( − 1 ) = 1 + ( − 1 ) 3 + ( − 1 ) 5 + ( − 1 ) 7 + … + ( − 1 ) 101 = 1 + ( − 1 ) + ( − 1 ) + … + ( − 1 ) ⏟ 50 : 0 ( − 1 ) = 1 + 50. ( − 1 ) = 1 − 50 = − 49 Vây f ( 1 ) = 51 ; f ( − 1 ) = − 49
Chọn đáp án B
23 tháng 3 2022
a.\(P\left(x\right)=1+3x^5-4x^2+x^5+x^3-x^2+3x^3\)
\(=1-5x^2+4x^3+4x^5\)
\(Q\left(x\right)=2x^5-x^2+4x^5-x^4+4x^2-5x\)
\(=-5x+3x^2+3x^4+2x^5\)
b.\(P\left(x\right)+Q\left(x\right)=1-5x^2+4x^3+4x^5-5x+3x^2+3x^4+2x^5\)
\(=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(P\left(x\right)-Q\left(x\right)=1-5x^2+4x^3+4x^5+5x-3x^2-3x^4-2x^5\)
\(=2x^5-3x^4+4x^3-8x^2+5x+1\)
c.\(P\left(x\right)+Q\left(x\right)=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(x=-1\)
\(P\left(x\right)+Q\left(x\right)=6.\left(-1\right)^5+3.\left(-1\right)^4+4.\left(-1\right)^3-5.\left(-1\right)+1\)
\(=-6+3-4+5+1=-1\)
d.\(Q\left(0\right)=\)\(-5x+3x^2+3x^4+2x^5\)
\(=0\)
\(P\left(0\right)=\)\(1-5x^2+4x^3+4x^5\)
\(=1\)
Vậy x=0 ko là nghiệm của đa thức P(x)
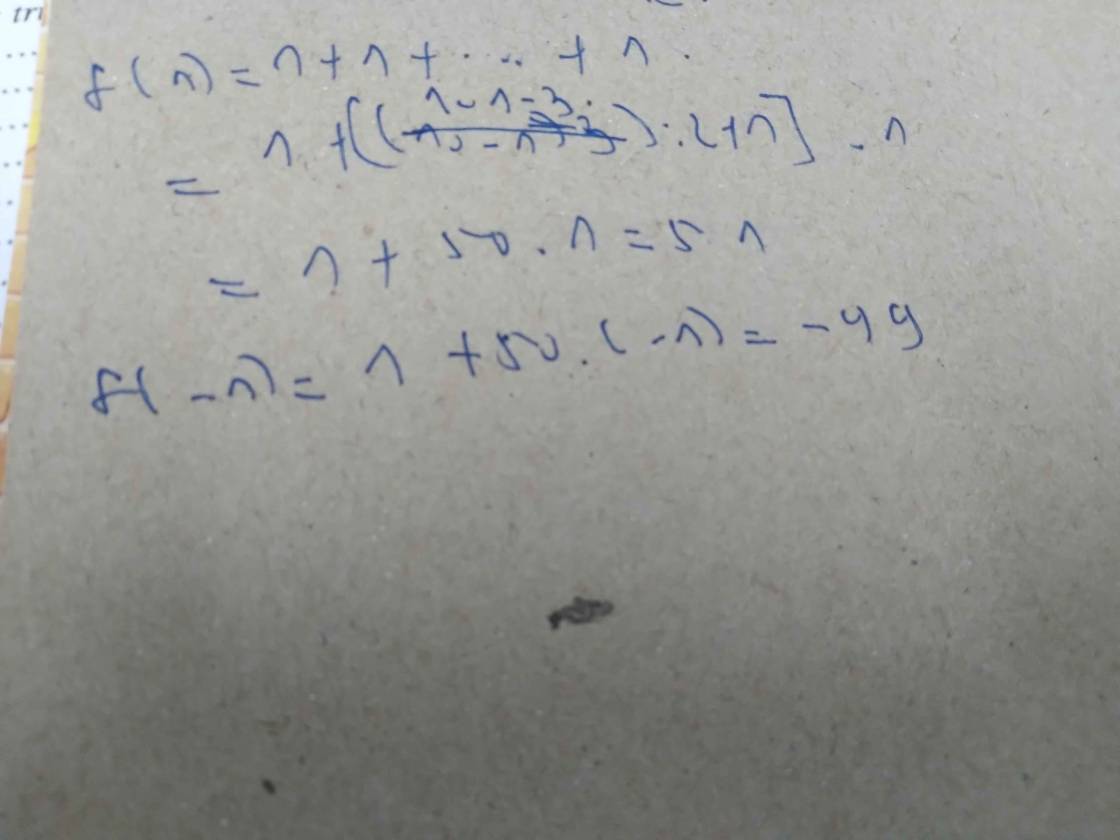
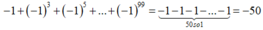
\(P\left(x\right)=x+x^3+x^5+x^7+...+x^{101}\)
Ta có: \(x=-1\text{ }\Rightarrow\text{ }x=x^3=x^5=x^7=...=x^{101}=-1\), thay vào đa thức \(P\left(x\right)\), ta có:
\(P\left(x\right)=\left(-1\right)\cdot51=-51\)
Vậy \(P\left(x\right)=-51\) khi \(x=-1\).
\(\text{안녕하세요}\)
Số số hạng của dãy \(\frac{101-1}{2}+1=51\)
Vì x=-1 và các số hạng trong đa thức P(x) đều mang mũ lẽ nên P(x)=(-1)+(-1)+(-1)+...+(-1) ( 51 số hạng ) = (-1) *51=-51
k mk nha