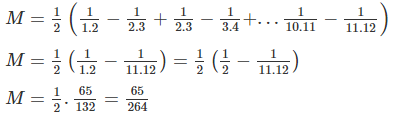BT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MT
5
MT
23 tháng 10 2015
bài này dễ thôi:
theo công thức của học sinh thi toán casio thì:
1.2.3+2.3.4+3.4.5+....+2013.2014.2015=\(\frac{2013.1014.2015.2016}{4}=.....tựtính\)
23 tháng 10 2015
= 1.2.3.4 + 2.3.4.(5 -1) + 3.4.5.(6 - 2) + 4.5.6.(7 - 3)+... + 2013.2014.2015.(2016-2012)
=1.2.3.4 + 2.3.4.5 - 1.2.3.4 + 3.4.5.6 - 2.3.4.5 + 4.5.6.7 - 3.4.5.6+... +2013.2014.2015.2016 - 2012.2013.2014.2015
=\(\frac{2012.2013.2014.2015}{4}\)
CB
1
DT
3
HP
9 tháng 5 2016
Tổng quát: \(\frac{2}{\left(a-1\right)a\left(a+1\right)}=\frac{1}{\left(a-1\right).a}-\frac{1}{a\left(a+1\right)}\)
Ta có: \(S=\frac{2}{1.2.3}+\frac{2}{2.3.4}+.....+\frac{2}{2013.2014.2015}\)
\(S=\left(\frac{1}{1.2}-\frac{1}{2.3}\right)+\left(\frac{1}{2.3}-\frac{1}{3.4}\right)+.....+\left(\frac{1}{2013.2014}-\frac{1}{2014.2015}\right)\)
\(S=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+....+\frac{1}{2013.2014}-\frac{1}{2014.2015}\)
\(S=\frac{1}{1.2}-\frac{1}{2014.2015}=\frac{1}{2}-\frac{1}{2014.2015}<\frac{1}{2}\)
Vậy....................
6 tháng 5 2016
S=(2/1.2-2/2.3)+(2/2.3-2/3.4)+(2/3.4-2/4.5)+...........+(2/2013.2014-2/2014-2/2015)
S=(2/1.2-2/2014.2015):2
S=1-2/2014.2/2015
--> S>1/2
CA
4
27 tháng 9 2018
A = 1.2 + 2.3 + ... + 99.100
3A = 1.2.3 + 2.3.(4-1) + ... + 99.100.(101-98)
3A = 1.2.3 + 2.3.4 - 1.2.3 + ... + 99.100.101 - 98.99.100
3A = 99.100.101
3A = 999900
A = 333300
C = 1.2.3 + 2.3.4 + ... + 49.50.51
4C = 1.2.3.4 + 2.3.4.(4-1) + ... + 49.50.51.(52-48)
4c = 1.2.3.4 + 2.3.4.5 - 1.2.3.4 + ... + 49.50.51.52 - 48.49.50.51
4C = 49.50.51.52
4C = 6497400
C = 1624350
NY
1
31 tháng 3 2019
\(M=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+.....+\frac{1}{10.11.12}\)
\(M=\frac{1}{2}-\frac{1}{11.12}\)
\(M=\frac{65}{132}\)
Ngắn gọn , xúc tích !!! :))
NK
5
1 tháng 5 2015
\(M=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{10.11}-\frac{1}{11.12}\)
\(=\frac{1}{2}-\frac{1}{11.12}\)
\(=\frac{65}{132}\)
1 tháng 5 2015
Ta có nhận xét: 1/1.2 - 1/2.3 = 3-1/1.2.3 = 2/1.2.3
1/2.3 - 1/3.4 = 4-2/2.3.4 = 2/2.3.4
Suy ra: 1/1.2.3 = 1/2(1/1.2 - 1/2.3)
1/2.3.4 = 1/2(1/2.3 -1/3.4)
Do đó: M = 1/2(1/1.2-1/2.3 + 1/2.3 -1/3.4 + ... + 1/10.11 -1/11.12)
= 1/2(1/1.2 - 1/11.12) = 1/2(1/2-11/12 )
= 1/2.65/132 = 65/264
Phức tạp lắm
AK
17 tháng 4 2018
\(S=\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{2013.2014.2015}\)
\(S=\frac{1}{2}.\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{2013.2014}-\frac{1}{2014.2015}\right)\)
\(S=\frac{1}{2}.\left(\frac{1}{1.2}-\frac{1}{2014.2015}\right)\)
\(S=\frac{1}{2}.\left(\frac{1}{2}-\frac{1}{4058210}\right)\)
\(S=\frac{1}{2}.\left(\frac{2029105}{4058210}-\frac{1}{4058210}\right)\)
\(S=\frac{1}{2}.\frac{2029104}{4058210}\)
\(S=\frac{1014552}{4058210}\)
Chúc bạn học tốt !!!
AK
17 tháng 4 2018
Công thức :
\(\frac{1}{2}.\left(\frac{1}{1.2}-\frac{1}{2.3}\right)=\frac{1}{2}.\left(\frac{1}{2}-\frac{1}{6}\right)=\frac{1}{2}.\left(\frac{3}{6}-\frac{1}{6}\right)=\frac{1}{2}.\frac{2}{6}=\frac{1}{6}=\frac{1}{1.2.3}\)
14 tháng 6 2020
\(A=\frac{4}{1.2}+\frac{4}{2.3}+\frac{4}{3.4}+...+\frac{4}{2019.2020}\)
\(\frac{1}{4}A=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2019.2020}\)
\(\frac{1}{4}A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2019}-\frac{1}{2020}\)
\(\frac{1}{4}A=1-\frac{1}{2020}=\frac{2019}{2020}\)
\(\Rightarrow A=\frac{2019}{2020}:\frac{1}{4}=\frac{2019}{505}\)
Vậy \(A=\frac{2019}{505}.\)
\(B=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{98.99.100}\)
\(\Rightarrow2B=\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{98.99.100}\)
\(2B=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{98.99}-\frac{1}{99.100}\)
\(2B=\frac{1}{1.2}-\frac{1}{99.100}=\frac{4949}{9900}\)
\(\Rightarrow B=\frac{4949}{9900}:2=\frac{4949}{19800}\)
Vậy \(B=\frac{4949}{19800}.\)
14 tháng 6 2020
\(A=\frac{4}{1\cdot2}+\frac{4}{2\cdot3}+\frac{4}{3\cdot4}+...+\frac{4}{2019\cdot2020}\)
\(A=4\left(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{2018\cdot2019}\right)\)
\(A=4\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2018}-\frac{1}{2019}\right)\)
\(A=4\left(1-\frac{1}{2019}\right)=4\cdot\frac{2018}{2019}\)
Đến đây tự tính
\(B=\frac{1}{1\cdot2\cdot3}+\frac{1}{2\cdot3\cdot4}+\frac{1}{3\cdot4\cdot5}+...+\frac{1}{98\cdot99\cdot100}\)
\(B=\frac{1}{2}\left(\frac{2}{1\cdot2\cdot3}+\frac{2}{2\cdot3\cdot4}+\frac{2}{3\cdot4\cdot5}+...+\frac{2}{98\cdot99\cdot100}\right)\)
\(B=\frac{1}{2}\left(\frac{1}{1\cdot2}-\frac{1}{2\cdot3}+\frac{1}{2\cdot3}-\frac{1}{3\cdot4}+...+\frac{1}{98\cdot99}-\frac{1}{99\cdot100}\right)\)
\(B=\frac{1}{2}\left(\frac{1}{2}-\frac{1}{99\cdot100}\right)=\frac{1}{2}\left(\frac{1}{2}-\frac{1}{9900}\right)\)
Số hơi bị dữ nên tính nốt nhé