
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MD
0

Các câu hỏi dưới đây có thể giống với câu hỏi trên

6 tháng 11 2021
Tự túc là hạnh phúc nha bn chứ mk nói thật luôn là cho dù có bt lm thì cx chẳng ai dư hơi giúp bn giải mấy cái đề này đâu
DC
0

M
0

CP
0

LV
0

LB
0

LB
1
LB
0

LB
1

DD
Đoàn Đức Hà
Giáo viên
7 tháng 11 2021
Gọi số viên bi xanh, đỏ, vàng lần lượt là: \(a,b,c\)(viên) \(a,b,c\inℕ^∗\).
Vì tổng số bi là \(35\)viên nên \(a+b+c=35\).
Vì số bi xanh và đỏ tỉ lệ với \(2\)và \(3\)nên \(\frac{a}{2}=\frac{b}{3}\Leftrightarrow\frac{a}{8}=\frac{b}{12}\).
Vì số bi đỏ và vàng tỉ lệ với \(4\)và \(5\)nên \(\frac{b}{4}=\frac{c}{5}\Leftrightarrow\frac{b}{12}=\frac{c}{15}\).
Suy ra \(\frac{a}{8}=\frac{b}{12}=\frac{c}{15}\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{8}=\frac{b}{12}=\frac{c}{15}=\frac{a+b+c}{8+12+15}=\frac{35}{35}=1\)
\(\Leftrightarrow\hept{\begin{cases}a=1.8=8\\b=1.12=12\\c=1.15=15\end{cases}}\)
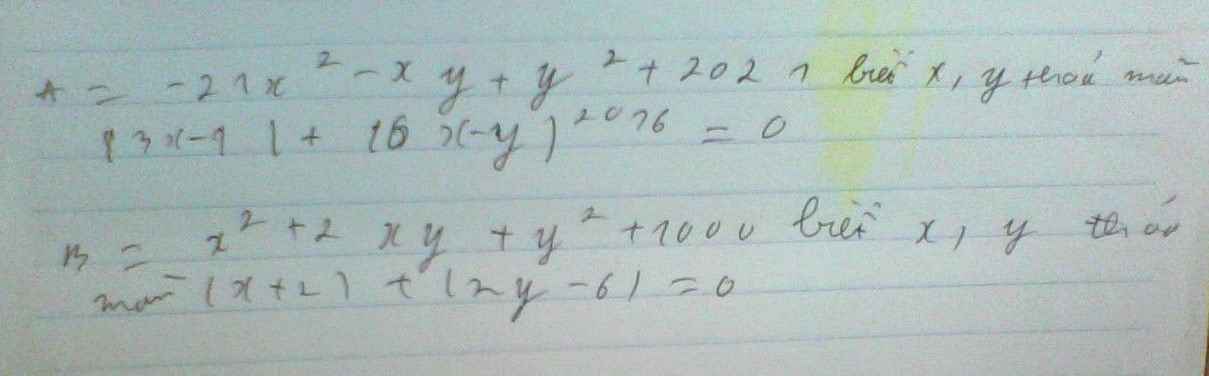




 Thực hiện phép tính
Thực hiện phép tính



 các bạn giúp mình với mình đang cần gấp
các bạn giúp mình với mình đang cần gấp

