
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ A= 1-3+5-7+9-11+......+97-99
= -2+(-2)+(-2)+......+(-2)
= (-2).25=-50
b/B=-1-2-3-4-...-100
=-(1+2+3+4+...+100)
=-5050
c/C=1-2+3-4+5-6+......+99-100
= -1+(-1)+(-1)+.............+(-1)
=(-1).50=-50
d/D=1-2-3+4+5-6-7+8+9-....+94-95
= (1-2-3+4)+(5-6-7+8)+.......+(92-93-94+95)
= 0+0+0+...+0=0

\(P=\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\)
\(\Rightarrow\dfrac{1}{2}P=\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{101}}\)
\(\Rightarrow\dfrac{1}{2}P-P=\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{101}}-\dfrac{1}{2^2}-\dfrac{1}{2^3}-...-\dfrac{1}{2^{100}}\)
\(\Rightarrow-\dfrac{1}{2}P=\dfrac{1}{2^{101}}-\dfrac{1}{2^2}\)
\(\Rightarrow P=\left(\dfrac{1}{2^{101}}-\dfrac{1}{2^2}\right):\left(-\dfrac{1}{2}\right)\)

D = 1 − 2 − 3 + 4 + 5 − 6 − 7 + ... + 97 − 98 − 99 + 100 = 1 − 2 + − 3 + 4 + 5 − 6 + ... + 97 − 98 + − 99 + 100 = − 1 + 1 + − 1 + ... + − 1 + 1 = − 1 + 1 + − 1 + 1 + ... + − 1 + 1 − 1 = 0 + 0 + ... + 0 − 1 = − 1.


C = ( \(\dfrac{1}{2}\) - 1).(\(\dfrac{1}{3}\) - 1).( \(\dfrac{1}{4}-1\)).....(\(\dfrac{1}{100}\) - 1)
C = ( - \(\dfrac{1}{2}\)).(-\(\dfrac{2}{3}\)).(\(-\dfrac{3}{4}\))........(\(-\dfrac{99}{100}\))
Tủ số các phân số có trong tích C là các số thuộc dãy số sau:
1; 2; 3; 4; .....;99
Dãy số trên có số số hạng là: ( 99- 1) : 1 + 1 = 99
Vậy tích C là tích của 99 phân số âm nên tích C là một số âm
C = - ( \(\dfrac{1}{2}.\dfrac{2}{3}.\) \(\dfrac{3}{4}\)...........\(\dfrac{99}{100}\))
C = - ( \(\dfrac{2.3.4.5.6...99}{2.3.4.5.6...99}\) \(\times\) \(\dfrac{1}{100}\))
C = - ( 1 \(\times\) \(\dfrac{1}{100}\))
C = - \(\dfrac{1}{100}\)
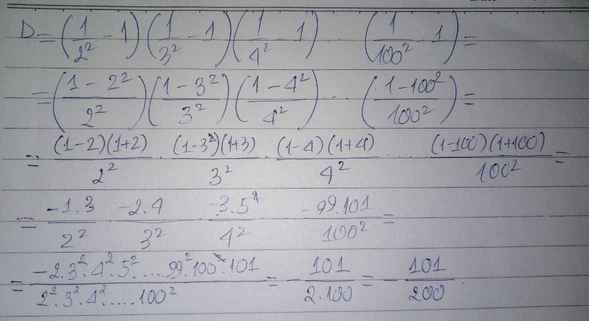
Để tính giá trị biểu thức D, ta có thể sử dụng công thức D = 1/(2^2 * 3^2 * 4^2 * ... * 100^2). Khi đó, ta cần tính trước tử số là tích của các số 1/2^2, 1/3^2, 1/4^2,..., 1/100^2.
Cách tính tử số này như sau:
Ta lấy 1/2^2 đưa trước, rồi nhân tiếp với 1/3^2, 1/4^2, ..., 1/100^2 lần lượt.
Tương tự như vậy, ta cũng có thể lấy 1/4^2 đưa trước, rồi nhân tiếp với các số còn lại.
Hoặc ta có thể tính tử số bằng cách lấy 1/2 nhân cho 1/2, rồi lấy kết quả nhân tiếp với 1/3, 1/4, ..., 1/100 (tức là nhân tử số của các phân số này với nhau).
Để tính nhanh hơn, ta có thể sử dụng trong hoặc sử dụng công thức nhân phân số:
1/2^2 = 1/4
1/3^2 = 1/9
Vậy tử số có thể viết dưới dạng 1/(4 * 9 * 16 * ... * 10000).
Từ đó, ta có thể viết lại biểu thức D là D = 1/(2^2 * 3^2 * 4^2 * ... * 100^2) = 1/(4 * 9 * 16 * ... * 10000).
Từ đó ta thấy, tử số và mẫu số trong biểu thức này đều có tính chất là các bình phương của các số tự nhiên liên tiếp. Vì vậy, ta có thể dùng công thức tổng quát để tính tổng các bình phương của các số tự nhiên:
S = 1^2 + 2^2 + 3^2 + ... + 100^2 = (100 * 101 / 2)^2 (đây là một kết quả quen thuộc trong toán học, gọi là công thức cộng dồn bình phương).
Do đó, ta có thể tính được giá trị của biểu thức D bằng cách:
D = 1/(4 * 9 * 16 * ... * 10000) = 1/((2^2 * 3^2 * ... * 100^2) / (2 * 4 * 6 * ... * 200)) = 1/[(S / 4) / 2 * 4 * 6 * ... * 200] = (2 * 4 * 6 * ... * 200)^2 / S
Vậy giá trị của biểu thức D là:
D = (2 * 4 * 6 * ... * 200)^2 / S = [2 * 4 * 6 * ... * 200 * 100 / (1 * 3 * 5 * ... * 99)]^2 / (100 * 101 / 2)^2 = [2^50 * 100! / (1! * 3! * 5! * ... * 99!)]^2 / (100 * 101)^2
Ở đây, dấu "!" đọc là "giai thừa". Ta đã sử dụng tích lẻ với công thức (2n-1)!! = 1 * 3 * 5 * ... * (2n-1) để tính 1! * 3! * 5! * ... * 99!.
Cách tính trên không cần tìm giá trị cụ thể của các phân số riêng lẻ, mà chỉ cần tính tử số và mẫu số chung của biểu thức D.