Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}\).(7+9).4=32 cm2
Gọi hình thang với các số liệu nêu trên là hình thang ABCD, trong dó AB là đáy nhỏ, BC là đáy lớn (AB//CD). Giả sử cạnh bên có độ dài =8 cm là cạnh AD, góc ADC=300.
- Kẻ AH vuông góc với CD (H thuộc CD).
=>góc ADH = góc ADC=300
Xét tam giác AHD vuông tại H (do AH vuông góc với CD)
có: sinADH=\(\dfrac{AH}{AD}\)
=>AH=sinADH.AD=sin(30).AD=\(\dfrac{1}{2}\).8=4(cm)
Diện tích hình thang ABCD là:
SABCD=\(\dfrac{1}{2}.\left(7+9\right).4\)=32 cm2

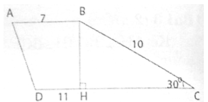
Giả sử hình thang ABCD (AB // CD) có AB = 7cm, BC = 10cm, CD = 11cm và
Kẻ BH ⊥ CD (H ∈ CD) Tam giác BHC vuông tại H lại có ∠C = 30o nên tam giác BHC là nửa tam giác đều. Suy ra
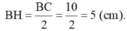
Diện tích hình thang ABCD là:
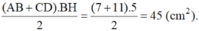

Bài này có 2 cách nhưng mình chỉ giải 1 cách thôi,không biết có đúng không nhé!(Cho phép mình đặt tên các đỉnh)
Kẻ BE//AD =>Tam giác BEC là tam giác vuông.Vì góc BCE = 45 độ
=> Góc CBE= 45 độ =>Tam giác BEC vuông cân.=> BE=EC=DC-DE=9-6=3.
Diện tích của hình thang là:(a+b)*h:2=(AB+CD)*BE:2=(6+9)*3:2=45:2=22.5(cm vuông)

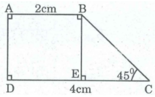
Giả sử hình thang vuông ABCD có:
∠ A = ∠ D = 90 0 ; ∠ C = 45 0
Kẻ BE ⊥ CD
Tam giác vuông BEC có ∠ (BEC) = 90 0 cân tại E ⇒ BE = EC
Hình thang ABCD có hai cạnh bên AD // BE (vì cùng vuông góc với DC) ⇒ DE = AB = 2cm
EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm ( vì tam giác BEC là tam giác vuông cân).
SABCD = 1/2 .BE(AB+ CD) = 1/2 .2.(2 + 4) = 6 ( c m 2 )

Áp dụng định lý Pythagore vào tam giác vuông \(ADE\) ta có:
\(D{E^2} + A{E^2} = A{D^2}\)
\(D{E^2} = A{D^2} - A{E^2} = {61^2} - {60^2} = 121 = {11^2}\)
\(DE = 11\) (cm)
Độ dài \(AB\) là: \(92 - 11.2 = 70\) (cm)
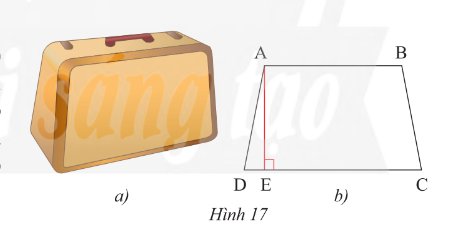
Tam giac ABC la nua tam giac deu.
Chieu cao hinh thang la AC=8/2=4 (cm)
Dien h hinh thang la S=\(\frac{\left(7+9\right)}{2}4\)=32 (cm vuong)
Võ Nhật Lê sai rồi nếu tam giác ABC là nữ tam giác đêu thì AB=2BC mới đúng chứ ko phải là AB=2AC