Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp giải:
Tìm hoành độ giao điểm, áp dụng công thức tính diện tích giới hạn bởi hai đồ thị hàm số
Lời giải:
Hoành độ giao điểm của ( P 1 ) , ( P 2 ) là nghiệm của phương trình:
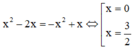
Vậy diện tích cần tính là
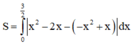
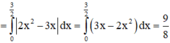

Phương trình hoành độ giao điểm của hai đường cong là
x 2 + x - 1 = x 4 + x - 1 ⇔ x 2 - x 4 = 0 ⇔ x ∈ 0 ; 1 ; - 1
Khi đó diện tích cần tìm là
S = ∫ - 1 1 x 2 - x 4 d x = ∫ - 1 0 x 2 - x 4 d x + ∫ 0 1 x 2 - x 4 d x = x 3 3 - x 5 5 - 1 0 + x 3 3 - x 5 5 0 1 = 4 15
Đáp án A
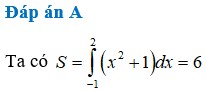


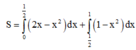
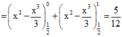

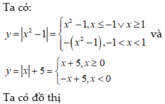

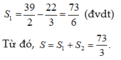
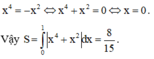
a) Phương trình hoành độ giao điểm f(x) = X2 - x - 2 =0 ⇔ x = -1 hoặc x = 2.
Diện tích hình phẳng cần tìm là :
b) Phương trình hoành độ giao điểm:
f(x) = 1 - ln|x| = 0 ⇔ lnx = ± 1
⇔ x = e hoặc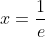
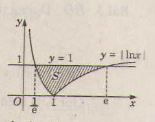
y = ln|x| = lnx nếu lnx ≥ 0 tức là x ≥ 1.
hoặc y = ln|x| = - lnx nếu x < 0, tức là 0 < x < 1.
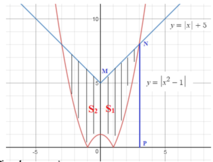
Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :
Ta có ∫lnxdx = xlnx - ∫dx = xlnx – x + C, thay vào trên ta được :
c) Phương trình hoành độ giao điểm là:
f(x) = 6x – x2 – (x - 6)2 = -2(x2 – 9x +18)
f(x) = 0 ⇔ -2(x2 – 9x +18) ⇔ x = 3 hoặc x = 6.
Diện tích cần tìm là:
Ths