
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\) \(AC^2=BC^2-AB^2\)
\(\Leftrightarrow\) \(AC^2=10^2-6^2=64\)
\(\Leftrightarrow\) \(AC=\sqrt{64}=8\)cm
b) Xét \(\Delta ABC\) và \(\Delta BDA\)có:
\(\widehat{BAC}=\widehat{DBA}=90^0\)
\(\widehat{ACB}=\widehat{BAD}\) (cùng phụ với góc DAC)
suy ra: \(\Delta ABC~\Delta BDA\)
c) \(\Delta ABC~\Delta BDA\)
\(\Rightarrow\)\(\frac{S_{ABC}}{S_{BDA}}=\left(\frac{AC}{AB}\right)^2=\left(\frac{8}{6}\right)^2=\left(\frac{4}{3}\right)^2=\frac{16}{9}\)

1: Xét ΔABC có BD là đường phân giác
nên AD/CD=AB/BC=3/5
2: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
\(\widehat{C}\) chung
do đó: ΔCHD∼ΔCAB
Suy ra: HD/AB=CD/CB
hay \(CD\cdot AB=HD\cdot CB\)

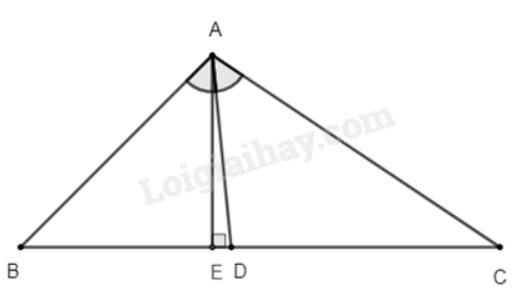
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).

1: Xét tứ giác ADME co
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
Xét ΔABC có
DM//AC
nên DM/AC=BD/BA=BM/BC
=>D là trung điểm của BA
Xét ΔABC có ME//AB
nên ME/AB=CM/CB=CE/CA=1/2
=>E là trung điểm của AC
=>EM//BD và EM=BD
=>BMED là hình bình hành
Xét tứ giác DMCE có
DM//CE
DM=CE
Do đó: DMCE là hình bình hành
2: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
AD=AB/2=3cm
AE=AC/2=4cm
\(S_{ADME}=3\cdot4=12\left(cm^2\right)\)
3: ΔHAC vuông tại H
mà HE là trung tuyến
nên HE=AC/2=MD
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Xét tứ giác DHME có
DE//MH
MD=HE
Do đo: DHME là hình thang cân


a) Gọi số cạnh của đa giác đều là n
Một góc trong của đa giác đều n-cạnh có số đo là

Tổng số đo các góc ngoài của đa giác đều n-cạnh là 360o
Ta có:
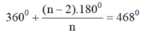
=> n(360o + 180o - 468o) = 360o
<=> n.72o = 360o
<=> n = 5
Vậy đa giác đều có 5 cạnh.
b) Ta có: AB2 + AC2 = BC2 (Py-ta-go)
<=> 62 + AC2 = 102
=> AC2 = 64 => AC = 8 (cm)
Diện tích tam giác ABC là: (6.8)/2 = 24 (cm2)

ta co: AB2+AC2=100 Ma BC2=100
\(\Rightarrow\Delta ABC\)vuong tai A
A, Trong \(\Delta ABC\)co AD la phan giac
\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\)(tinh chat duong phan giac)
\(\Rightarrow\frac{AB}{AB+AC}=\frac{BD}{BD+DC}\)\(\Rightarrow\frac{8}{8+6}=\frac{BD}{10}\Rightarrow BD=\frac{8.10}{14}=\frac{40}{7}cm\)
ta co: BD+DC=BC\(\Rightarrow DC=BC-BD=10-\frac{40}{7}=\frac{30}{7}cm\)
B, Ke duong cao AH
ta co: \(S_{\Delta ABD}=\frac{1}{2}AH.BD\)va \(S_{\Delta ACD}=\frac{1}{2}AH.DC\)
\(\Rightarrow\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}=\frac{40}{7}:\frac{30}{7}=\frac{4}{3}\)

Vì M là trung điểm của AB nên:
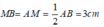
Áp dụng định lí py tago vào tam giác ABC có:
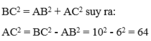
Suy ra: AC = 8cm
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và
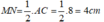
Suy ra: tứ giác MNCA là hình thang vuông.
Diện tích hình thang MNCA là:
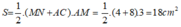
Chọn đáp án D
Áp dụng định lý Py - ta -go vào tam giác vuông ABC , ta có :
AC^2 = BC^2 - AB^2 = 10^2 - 6^2 = 64
-> AC = 8 (cm)
Diện tích tam giác ABC bằng :
1/2.AB.AC = 1/2.6.8 = 24 (cm^2)
Vậy diện tích tam giác ABC bằng 24 cm^2
bạn hoc o truong nao zay