Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

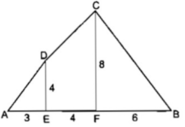
Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.
S A E D = 1/2 AE.DE = 1/2. 3. 4 = 6( c m 2 )
S E D C F = (ED + FC)/2. EF = (4 + 8)/2. 4 = 24 ( c m 2 )
S C F B = 1/2 CF. FB = 1/2 .8 .6 = 24 ( c m 2 )
S A B C D = S A E D + S E D C F + S C F B = 6 + 24 + 24 = 54 ( c m 2 )

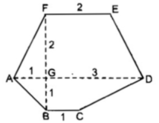
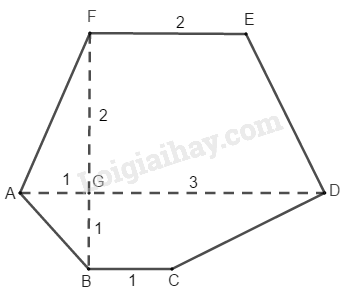
Ta chia đa giác ABCDEF thành hai hình thang ABCD và ADEF.
Hình thang ABCD có cạnh đáy BC = 1 (cm)
Đáy AD = AG + GD = 1 + 3 = 4 (cm)
Đường cao BG = 1 (cm)
S A B C D = (AD + BC) / 2.FG = (4 + 1) / 2 = 5/2 ( c m 2 )
Hình thang ADEF có đáy AD = 4 (cm)
S A D E F = (AD + EF) / 2.FG = (4 + 2) / 2. 2 = 6 ( c m 2 )
S A B C D E F = S A B C D + S A D E F = 5/2 + 6 = 17/2 ( c m 2 )
Đáy EF = 2cm, đường cao FG = 2cm

Diện tích đa giác ABCDEF là:
\(S_{ABCDEF}=S_{FGA}+S_{FEDG}+S_{BCDG}+S_{AGB}\\ =\dfrac{2.1}{2}+\dfrac{\left(2+3\right).2}{2}+\dfrac{\left(1+3\right).1}{2}+\dfrac{1.1}{2}\\ =1+5+2+0,5\\ =8,5\left(cm^2\right)\)
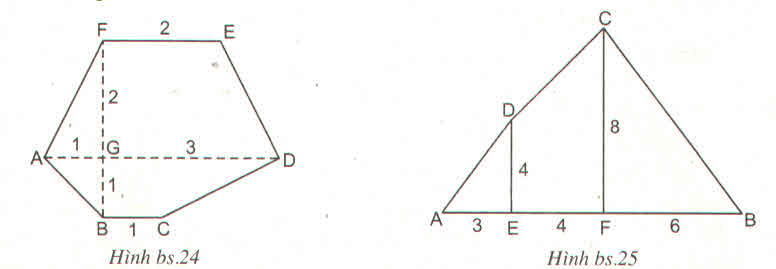
Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)