ND
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 8 2016
Hinh thang ABCD ( AB // CD ) nên góc B + góc C = 180 độ (1) ( hai góc trong cùng phái bù nhau )
ta lại có : góc B - góc C = 60 độ ( 2).
Cộng vế với vế (1) và (2) ta được : 2B = 240 độ => B = 120 độ => C = 60 độ
tương tự: Góc A + góc D = 180 (3) độ .
mà góc D = 4/5 góc A . thế vào (3) ta được: 9/5A = 180 độ => A = 100 độ => D = 80 độ
NM
Nguyễn Minh Quang
Giáo viên
3 tháng 9 2021
do AB song song với CD nên ta có \(A+D=180^0\text{ mà }A=D+40^0\Rightarrow D+40^0+D=180^0\Rightarrow\hept{\begin{cases}D=70^0\\A=110^0\end{cases}}\)
\(\Rightarrow C=\frac{A}{2}=55^0\Rightarrow B=180^0-55^0=125^0\)
CM
8 tháng 1 2017
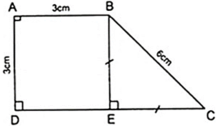
Xét hình thang cân ABCD ( AB//CD ) có Dˆ = 600
Theo định nghĩa và giả thiết về hình thang cân ta có: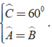 
Do góc A và góc D là hai góc cùng nằm một phía của
NN
6 tháng 9 2020
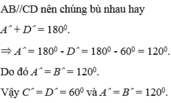
a) Vì ABCD là hình thang ( \(AB//CD\))
\(\Rightarrow\widehat{B}+\widehat{C}=180^o\)
mà \(\widehat{B}-\widehat{C}=50^o\)\(\Rightarrow\widehat{B}=\frac{180^o+50^o}{2}=115^o\)
\(\Rightarrow\widehat{C}=180^o-115^o=65^o\)
Vì \(AB//CD\)\(\Rightarrow\widehat{A}+\widehat{D}=180^o\)
mà \(\widehat{A}=\frac{1}{3}.\widehat{D}\)\(\Rightarrow\frac{1}{3}.\widehat{D}+\widehat{D}=180^o\)
\(\Rightarrow\frac{4}{3}.\widehat{D}=180^o\)\(\Rightarrow\widehat{D}=135^o\)\(\Rightarrow\widehat{A}=\frac{1}{3}.135^o=45^o\)
Vậy \(\widehat{A}=45^o\); \(\widehat{B}=115^o\); \(\widehat{C}=65^o\); \(\widehat{D}=135^o\)
6 tháng 9 2020
Vì ABCD là hình thang ( AB // CD )
\(\Rightarrow\hept{\begin{cases}\widehat{A}+\widehat{B}=180^o\\\widehat{C}+\widehat{D}=180^o\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{B}=\left(180+50\right):2=165^o\\\widehat{C}=165-50=95^o\end{cases}}\)
+) \(\widehat{A}=\frac{1}{3}\widehat{D}\)
\(\Rightarrow\widehat{D}=3\widehat{A}\)
\(\Rightarrow\widehat{A}+\widehat{D}=\widehat{A}+3\widehat{A}=4\widehat{A}=180^o\)
\(\Rightarrow\widehat{A}=180:4=45^o\)
\(\widehat{D}=3\widehat{A}=45.3=135^o\)
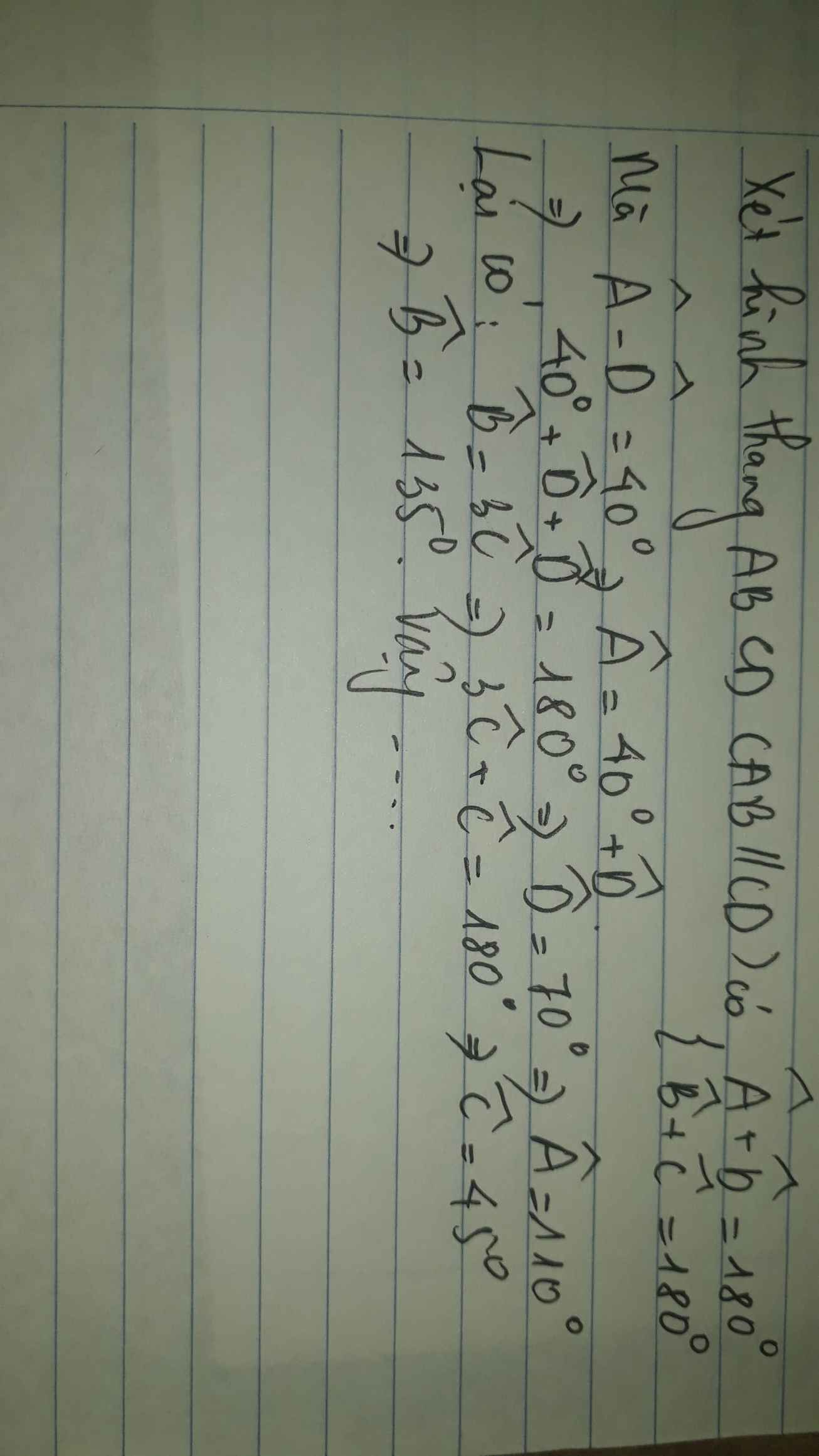
Vì ABCD là hình thang ( AB // CD )
⇒\hept{ˆA+ˆB=180oˆC+ˆD=180o⇒\hept{A^+B^=180oC^+D^=180o
⇒\hept{ˆB=(180+50):2=165oˆC=165−50=95o⇒\hept{B^=(180+50):2=165oC^=165−50=95o
+) ˆA=13ˆDA^=13D^
⇒ˆD=3ˆA