Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\widehat{A}=2\widehat{B}=6\widehat{C}\Leftrightarrow\frac{\widehat{A}}{2}=\frac{\widehat{B}}{6}=\frac{\widehat{C}}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có : \(\frac{\widehat{A}}{2}=\frac{\widehat{B}}{6}=\frac{\widehat{C}}{1}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{2+6+1}=\frac{180^o}{9}=20^o\)
\(\frac{\widehat{A}}{2}=20^o\Rightarrow\widehat{A}=20^o.2=40^o\)
\(\frac{\widehat{B}}{6}=20^o\Rightarrow\widehat{A}=20^o.6=120^o\)
\(\widehat{C}=20^o\)
Vậy ...
b,d tương tự

\(\dfrac{a}{b}=\dfrac{3}{4}\Leftrightarrow\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{2a-5b}{-14}=\dfrac{a-3b}{-9}=\dfrac{4a+b}{16}=\dfrac{8a-2b}{16}\\ \Leftrightarrow A=\dfrac{-14}{-9}-\dfrac{16}{16}=\dfrac{14}{9}-1=\dfrac{5}{9}\)

Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{2b}=\dfrac{2b}{c}=\dfrac{c}{a}=\dfrac{a+2b+c}{2b+c+a}=1\)
\(\dfrac{a}{2b}=1\Rightarrow a=2b\\ \dfrac{2b}{c}=1\Rightarrow c=2b\\ \dfrac{c}{a}=1\Rightarrow a=c\\ \Rightarrow a=2b=c\)
\(M=\dfrac{a^3.c^2.b^{2015}}{b^{2020}}=\dfrac{a^3.a^2}{b^5}=\dfrac{a^5}{b^5}=\dfrac{\left(2b\right)^5}{b^5}=\dfrac{32b^5}{b^5}=32\)

b) Ta có : \(\dfrac{2a}{3}=\dfrac{3b}{4}=\dfrac{4c}{5}\)
\(\Leftrightarrow\dfrac{a}{\dfrac{3}{2}}=\dfrac{b}{\dfrac{4}{3}}=\dfrac{c}{\dfrac{5}{4}}=\dfrac{a+b+c}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
Khi đó \(a=12.\dfrac{3}{2}=18;b=12.\dfrac{4}{3}=16;c=12.\dfrac{5}{4}=15\)
Vậy (a,b,c) = (18,16,15)
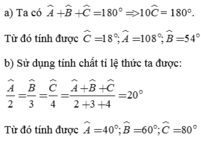
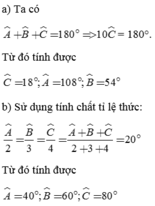
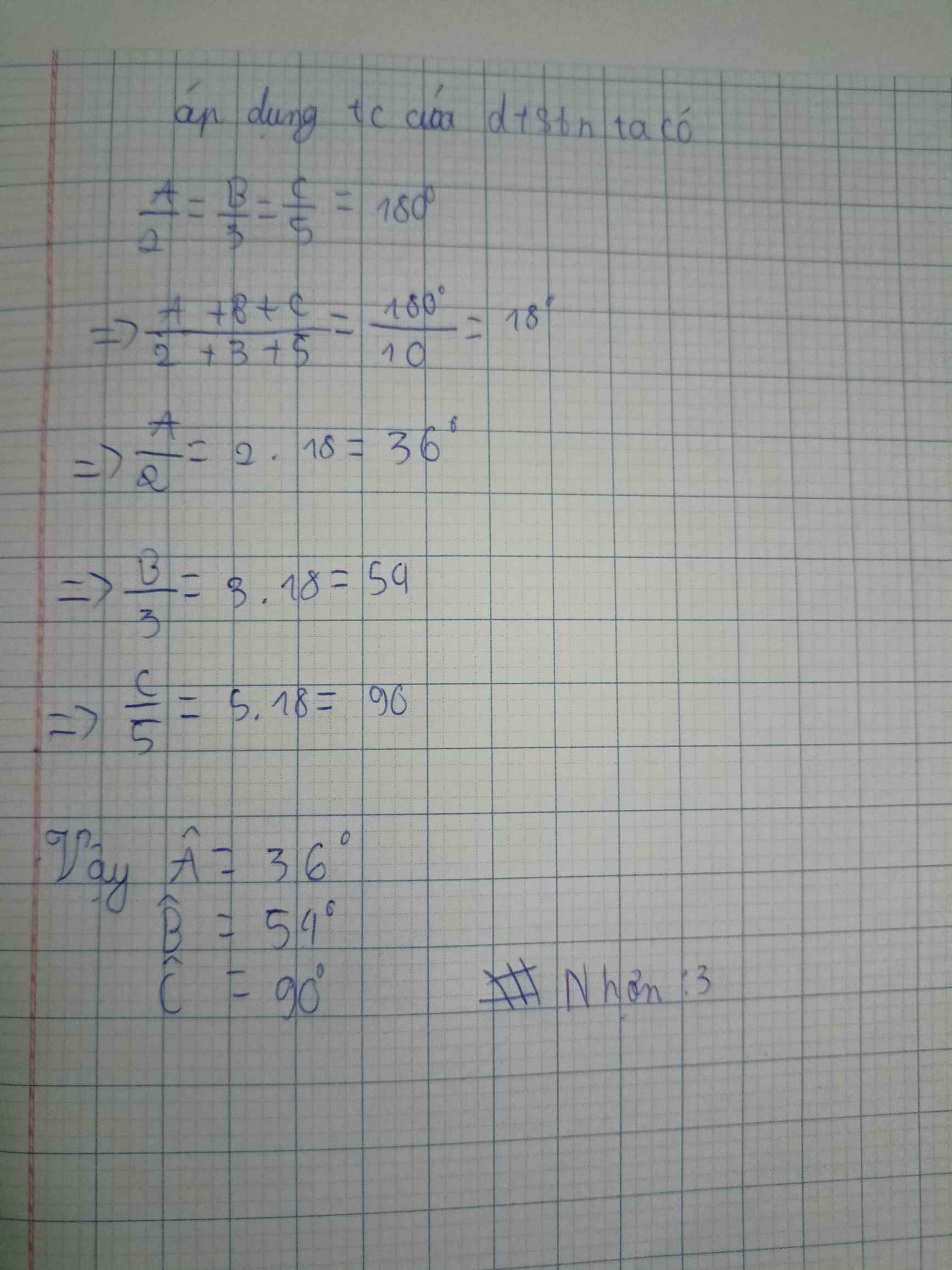
Lời giải:
a. Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{A}{3}=\frac{B}{4}=\frac{C}{5}=\frac{A+B+C}{3+4+5}=\frac{180^0}{12}=15^0$
$\Rightarrow A=3.15^0=45^0; B=4.15^0=60^0; C=5.15^0=75^0$
b. Áp dụng TCDTSBN:
$A=2B=6C$
$= A=\frac{B}{\frac{1}{2}}=\frac{C}{\frac{1}{6}}$
$=\frac{A+B+C}{1+\frac{1}{2}+\frac{1}{6}}=\frac{180^0}{\frac{5}{3}}=108^0$
$\Rightarrow A=108^0; B=108^0.\frac{1}{2}=54^0; C=108^0.\frac{1}{6}=18^0$