AL
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
9 tháng 7
Lời giải:
$S=10^2+(10.2)^2+(10.3)^2+...+(10.9)^2+(10.10)^2$
$=10^2(1^2+2^2+3^2+...+9^2+10^2)$
$=100.385=38500$
2 tháng 5 2018
:v cả chuyên mục câu hỏi hay :V
Câu 1:
Số số hạng của dãy là:
(99-1):1+1=99( số hạng)
Tổng của dãy trên là:
(99+1).99:2=4950
Câu 2:
Số hạng của dãy là:
(999-1):2+1=500 ( số hạng)
Tổng của dãy trên là:
(999+1).500:2=250000
Câu 3:
Số hạng của dãy là:
(998-10):2+1=495 ( số hạng)
Tổng của dãy trên là:
(998+10).495:2=249480
2 tháng 5 2018
Bài 1
Số số hạng = ( 99 - 1 ) : 2 + 1 = 99
B = ( 1 + 99 ) x 99 : 2 = 4950
Bài 2
Số số hạng = ( 999 - 1 ) : 2 + 1 = 500
C = ( 1 + 999 ) x 500 : 2 = 250000
Bài 3
Số số hạng = ( 998 - 10 ) : 2 + 1 = 495
D = ( 10 + 998 ) x 495 : 2 = 249480
21 tháng 6 2016
@duc7bthcsct tính thử rùi nhưng sợ sai nên hỏi cho chắc!
25 tháng 6 2019
1.ta có :
\(\left(10^3+10^2+10+1\right)^2\)
=\(\left(1111\right)^2\)
=1234321
hc tốt
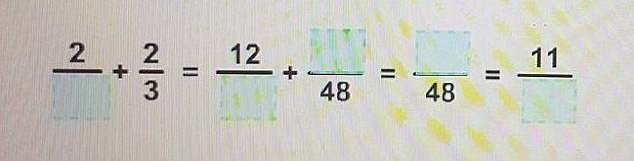
ai mà bấm máy tính đc
cái đoạn 1+2+3+4+...+1+2+3
chỗ ..... là đến số mấy z bạn