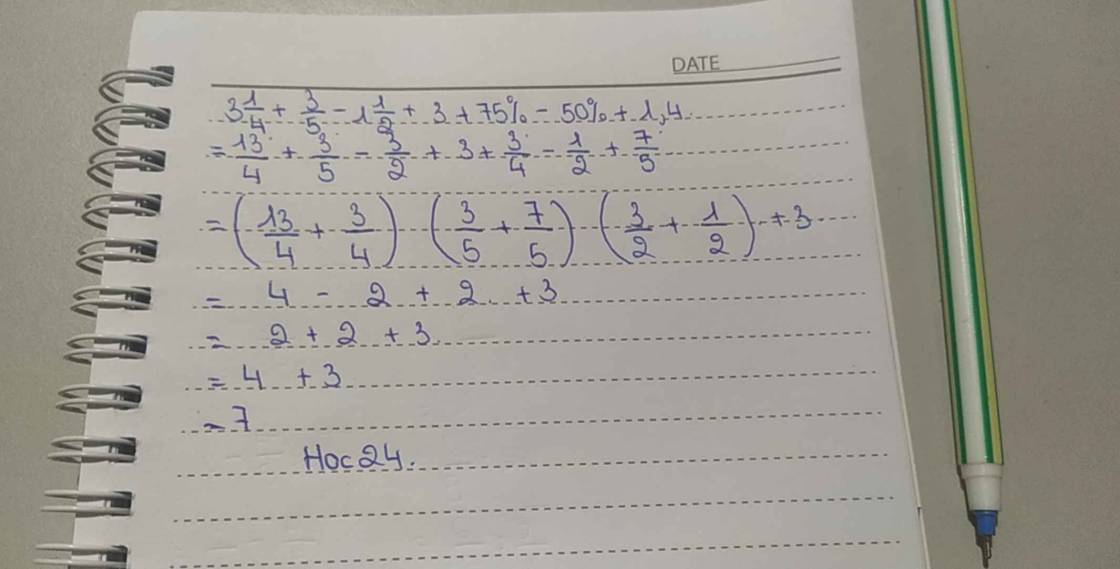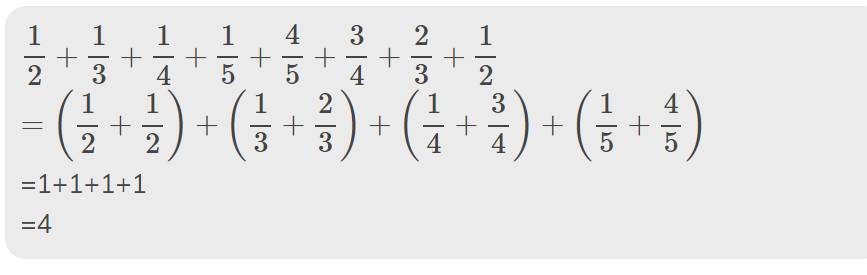Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1/2 + 1/3 + 1/4 + 1/5 + 4/5 + 3/4 + 2/3 + 1/2
= (1/2 + 1/2) + (1/3 + 2/3) + (1/4 + 3/4) + (1/5 + 4/5)
= 1 + 1 + 1 + 1
= 4
\(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{4}{5}+\dfrac{3}{4}+\dfrac{2}{3}+\dfrac{1}{2}\)
\(=\left(\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)+\left(\dfrac{1}{5}+\dfrac{4}{5}\right)\)
=1+1+1+1
=4

a) 2/3 : 3/5 × 5/7 : 2/3
= 2/3 × 5/3 × 5/7 × 3/2
= 25/21
b) 1 1/2 × 1 1/3 × 1 1/18 × 1 1/15 × 1 1/24 × 1 1/35
= 3/2 × 4/3 × 19/18 × 16/15 × 25/24 × 36/35
= 2 × 152/35 × 15/14
= 304/35 × 15/14
= 152/7

\(E=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)....\left(1-\frac{1}{2006}\right)\left(1-\frac{1}{2007}\right)\)
\(E=\frac{1}{2}.\frac{2}{3}....\frac{2005}{2006}.\frac{2006}{2007}\)
\(E=\frac{1.2.3.4...2005.2006}{2.3.4.5....2006.2007}\)
\(E=\frac{1}{2007}\)

\(\frac{5}{12}\times\frac{2}{3}+\frac{2}{3}\times\frac{7}{12}+\frac{1}{3}\)
\(=\frac{2}{3}\times\left(\frac{5}{12}+\frac{7}{12}\right)+\frac{1}{3}\)
\(=\frac{2}{3}\times1+\frac{1}{3}\)
\(=\frac{2}{3}+\frac{1}{3}\)
\(=1\)
\(\frac{5}{12}\times\frac{2}{3}+\frac{2}{3}\times\frac{7}{12}+\frac{1}{3}=\frac{2}{3}\times\left(\frac{5}{12}+\frac{7}{12}\right)+\frac{1}{3}\)
\(=\frac{2}{3}\times\frac{12}{12}+\frac{1}{3}=\frac{2}{3}\times1+\frac{1}{3}=\frac{2}{3}+\frac{1}{3}=\frac{3}{3}=1\)


\(=3.25+9.6-1.5+3+0.75-0.5+1.4\)
=3,25+0,75-2+3+11
=4+14-2
=2+14=16

1/2 + 1/3 + 1/4 + 1/5 + 4/5 + 3/4 + 2/3 + 1/2
= (1/2 + 1/2) + (1/3 + 2/3) + (1/4 + 3/4) + (1/5 + 4/5)
= 1 + 1 + 1 + 1
= 4

\(a,1\dfrac{4}{7}.3\dfrac{4}{11}.3\dfrac{11}{15}.5\dfrac{5}{8}\)
\(=\dfrac{11}{7}.\dfrac{27}{11}.\dfrac{56}{15}.\dfrac{45}{8}\)
\(=\dfrac{11.27.56.45}{7.11.15.8}\)
\(=\dfrac{1.3.7.3}{1.1.1.1}\)
\(=63\)
\(b,\dfrac{3}{4}.1\dfrac{1}{2}+\dfrac{3}{4}.\dfrac{1}{2}\)
\(=\dfrac{3}{4}.\left(1\dfrac{1}{2}+\dfrac{1}{2}\right)\)
\(=\dfrac{3}{4}.2\)
\(=\dfrac{3}{2}\)